Ej1. Sea X una variable aleatoria continua que tiene la siguiente función de densidad:
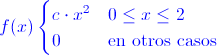
a) El valor de c para que f(x) sea una función de densidad.
b) Obtener la función de distribución.
c) Calcular: P(1 ≤ X ≤ 2).
d) Calcular la esperanza y la varianza de X.
e) Si X es la cantidad diaria vendida de un producto y la ganancia del vendedor es 5 unidades monetarias por cada unidad de producto vendida si X ≤ 1, y 8 unidades monetarias si X > 1, encontrar la ganancia esperada del vendedor para cualquier día especificado.
Apartado a)
Empleamos la expresión de función de densidad de probabilidad:
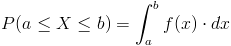
Para los intervalos expuestos en el enunciado del problema, en este caso:
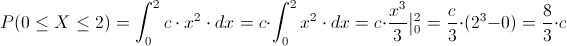
Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:
1. f(x) > 0,...para todo x.
2.
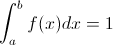
La función f(x) es mayor que cero, por lo que nos queda, satisfacer la primera condición:
(8/3)·c = 1
Y así, obtenemos el valor de c y la solución del problema, para que f(x) sea una función de densidad de probabilidad, el valor de c es de 3/8.
Por lo tanto, la función de densidad de la variable aleatoria continua X queda:
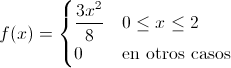
Apartado b)
Empleamos la expresión de función de distribución acumulada:
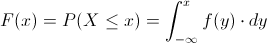
En nuestro caso, el intervalo que tenemos que realizar cálculos es 0 ≤ t ≤ x:
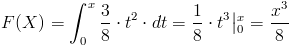
Ya que si x < .0, la función de distribución es 0, y si x > 2, la función de distribución es 1, por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:
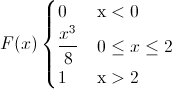
Apartado c)
Para calcular dicha probabilidad, empleamos la función de distribución acumulada tal y como se muestra a continuación:
P(1 ≤ X ≤ 2) = F(2) - F(1) = 2³/8 - 1³/8 = 7/8
Apartado d)
En este apartado, debemos calcular la esperanza y la varianza de la variable aleatoria continua, X.
Para el cálculo de la esperanza, empleamos la siguiente expresión:
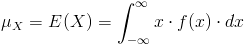
Por lo tanto, la esperanza de X, será:
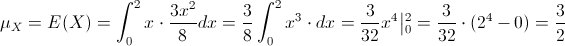
Y para la varianza, se empleará la siguiente expresión:
Var(X) = E(X²) - [E(X)]²
Por lo tanto:
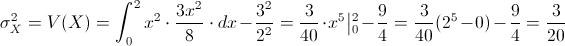
Apartado e)
Para este último apartado, nos dan otra función de la misma variable aleatoria continua X, tal que:
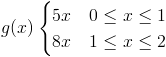
Nos piden la ganancia esperada del vendedor, para obtenerla, usamos la siguiente expresión:
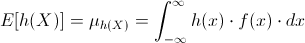
Por lo tanto:
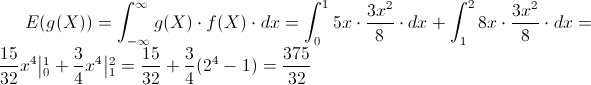





22 comentarios:
muy buen material de probabilidad y districuciones continuas...
recomendado 100%
Me alegra que te agrade dicho material.
Me ha sido de gran ayuda este material, muy buena exposición. Muchas gracias.
Hola Jaime:
Me alegra muchísimo que te haya sido de ayuda el material que expongo.
Un saludo
me vais a salvar la vida con esto, joe, que alivio, muchas gracias a todos
Muy buena página con muy buenos ejercicios resueltos. Muchas gracias, me han servido de mucha ayuda para mis proximos exámenes.
Prado
Me alegro que os haya servido la página para vuestros exámenes.
Un saludo.
SUPER CLARO ME ENCANTO LE ENTENDI MAS QUE A MI PROFESOR :s
Genio!! muchisimas gracias!! a patir de ahora estudio de acá para los parciales de la facu!!
Quiero felicitarte por tu página, es un gran aporte, me has salvado con estos ejercicios, espero que sigas aportando cosas así y muchas gracias :).
Buenas,
tengo una duda en el ejercicio 1, en el apartado b.
Tras la integral, te sale x^3/8, y luego dice que F(x) es:
- 0
- x^3/8
- 1
Dependiendo del valor de x. sin embargo, no entiendo de donde sale el 1. Es decir, en la función de densidad te dan los límites entre 0 y 2, ¿de donde sale el tercer valor (es decir el 1)?
Es más, si de la integral sólo te da el - x^3/8 , los otros dos valores de donde salen?
Muchas gracias por su inestimable ayuda,
Buenas:
Más que duda me parece que no tienes claro los conceptos ni qué es la función de distribución acumulada.
De forma breve y matemáticamente:
· Función de Probabilidad: Simplemente una curva.
· Función Acumulada: El área que encierra la curva de la función de probabilidad.
A partir de esto, nos pueden suceder cuatro casos:
· 1.- Un valor menor del definido por la función de probabilidad: Su integral es cero ya que no está dentro de la curva, por lo tanto, su valor acumulado es cero.
· 2.- Un valor único determinado de la curva: Su integral es cero (los límites se cancelan, no hay área), por lo tanto, su valor acumulado es también cero.
· 3.- Un intervalo comprendido en la curva de la función de probabilidad: Su integral es el área que encierra dicho intervalo, por lo tanto, su valor acumulado es el valor de dicha área.
· 4.- Un valor mayor que el definido por la curva de la función de probabilidad: Su integral es el área total de la curva, y como la función de probabilidad acumulada está definida desde 0 hasta 1, pues su valor acumulado es 1.
De manera estadística, más haya del límite superior definido por la función de probabilidad, no hablamos de que es más o menos probable, sino de que dicho evento sucede.
Un saludo y gracias por tu comentario.
Muchas gracias, efectivamente era un problema de entender el concepto.
Si mis profesores fuesen como usted..
Gracias de nuevo!!!
Hola,
tengo una duda en este ejercicio en el apartado c). Para calcular P(1≤X≤2) usted utiliza la función de distribución acumulada. Tomé apuntes en clase, y para calcular esto, utilizan la función de densidad, integrándola y poniendo como límites de la integral los valores de P.
Por ejemplo: si la función de densidad es:
-2x para x en [0,1]
- 0 para el resto
para calcular P(0.1 ó < y usted calcula =< ó <=, creo que ya ha contestado en el ejercicio 3 a esta duda, pero ¿aplica también a este caso, o al utilizar la función de densidad los límites deben ser estrictos?
Muchas felicidades por este blog.
Lo siento, pero no consigo que salga el comentario completo, así que por favor, obvíelo porque faltan datos.
Básicamente se trataba de preguntar si para calcular la probabilidad en un intervalo por ejemplo 1<X<3, se puede hallar la integral de la función de densidad usando como límites de integración 1,3. Usted utiliza la función de distribución acumulada. He probado sus ejercicios, haciéndolo con la integral de la función de densidad y me sale el mismo resultado pero no sé si esto se puede aplicar en todos los casos..
Gracias de nuevo y un saludo
Gracias por su ayuda.
Buenas:
Creo que tienes un cacao mental bestial. Vamos a ver, realizar la integral a la función de densidad se obtiene la probabilidad del suceso en el intervalo definido por la propia integral.
Cuando tu realizas la integral con unos límites definidos previamente (en tu caso desde 1 hasta 3), lo que estás haciendo no es más que un caso particular de la función de distribución acumulada.
La diferencia radica en que al obtener la función de distribución acumulada estás obteniendo cualquier posible valor de área que abarca la curva de la función de densidad.
Mientras que integrando con límites predefinidos la curva de densidad, sólo obtienes el valor de dicho intervalo.
Se recomienda siempre, obtener la función de distribución acumulada para así poder resolver cualquier probabilidad que te puedan requerir en el futuro, mientras que si sólo resuelves un intervalo delimitado, si te piden otra probabilidad, deberás integrar de nuevo, la curva de densidad.
En resumen, lo que estas haciendo es un caso concreto (limitado por los límites de integración) de la distribución acumulada. Es por ello que siempre deben de coincidir el resultado final.
Un saludo y gracias por tu comentario.
Q bacano amigo...la forma como se explican aca los ejercicios estoy felizzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz ya pude entender mucho masssssssssssssssssssssssssssssssssss....Gracias mil gracias....creo q me toca aprender un poco mas saber integrar para no embarrarla...Dios lo bendiga amigo
Muy buen material! Felicitaciones
ESTA ESPECTACULAR ESTE MATERIAL...ME SIRVIO DEMASIADO........MUCHAS GRACIAS :)
Buenas:
Me alegro que os sea de utilidad los contenidos que en este blog, Aqueronte, exponemos.
Un saludo y gracias por tu comentario.
Muy buen ejemplo y muy bien explicado.
hola, tengo una duda en el apartado e).
De donde sale el 2 de 12
Publicar un comentario