Ej3. Sea X una variable aleatoria continua que mide el avance entre dos automóviles consecutivos elegidos al azar en segundos, su función de distribución del tiempo de avance presenta la forma:
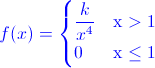
Hallar:
a) Determinar el valor de k para que f(x) sea una función de densidad legítima.
b) Obtener la función de distribución acumulada.
c) Calcular: P(X > 2) y P(2 < . X < . 3).
d) Obtener el valor medio y la desviación estándar del avance.
Apartado a)
Empleamos la expresión de función de densidad de probabilidad:
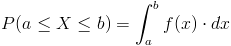
Para los intervalos expuestos en el enunciado del problema, en este caso:
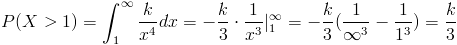
Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:
1. f(x) > 0,...para todo x.
2.
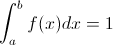
La función f(x) es mayor que cero, para ello, k debe ser mayor que cero, por lo que nos queda, satisfacer la primera condición:
k/3 = 1
Y así, obtenemos el valor de k y la solución de este apartado, para que f(x) sea una función de densidad de probabilidad, el valor de k es de 3.
Por lo tanto, la función de densidad de la variable aleatoria continua X queda:
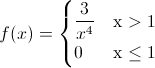
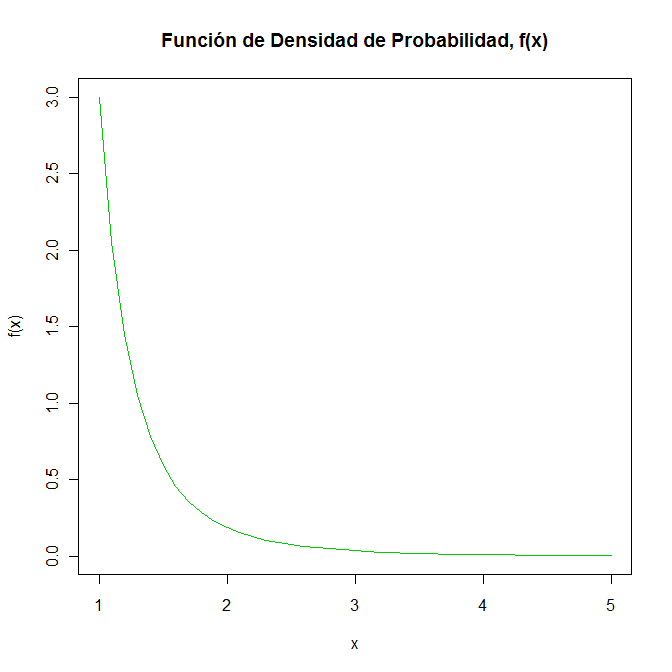
La representación gráfica de la función de densidad de probabilidad, f(x), se muestra a continuación:
Apartado b)
Empleamos la expresión de función de distribución acumulada:
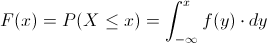
En nuestro caso, el intervalo que tenemos que realizar cálculos es X > 1:
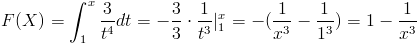
Por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:
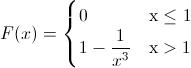
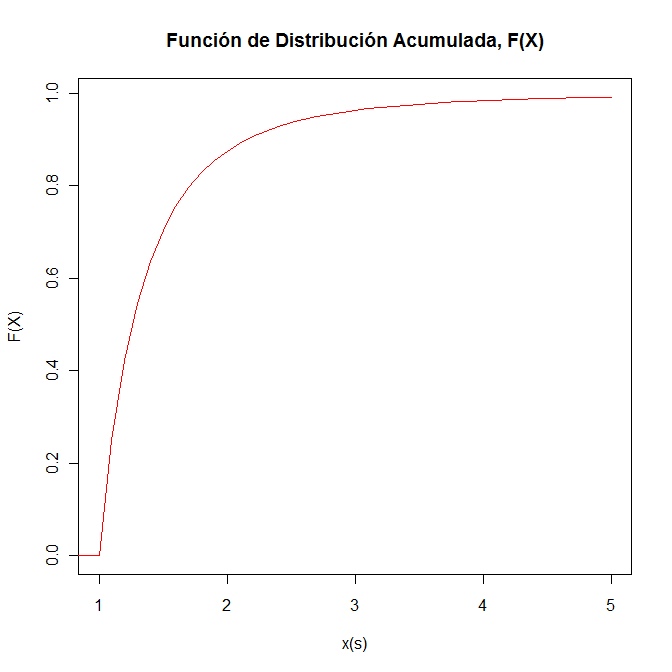
La representación gráfica de la función de distribución acumulada F(X) se muestra en la siguiente figura:
Para calcular las probabilidades de este apartado, empleamos la función de distribución acumulada tal y como se muestra a continuación:
· P(X > 2) = 1 - P(X ≤ 2) = 1 - F(2) = 1 - (1 - 1/2³) = 1/8
· P(2 ≤ X ≤ 3) = F(3) - F(2) = (1 - 1/3³) - (1 - 1/2³) = 19/216
Apartado d)
En este apartado, debemos calcular la esperanza y la desviación estándar de la variable aleatoria continua, X.
Para el cálculo de la esperanza, empleamos la siguiente expresión:
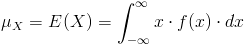
Por lo tanto, la esperanza de X, será:
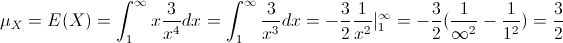
Y para la varianza, se empleará la siguiente expresión:
Var(X) = E(X²) - [E(X)]²
Por lo tanto:
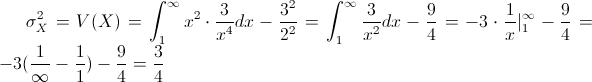
Una vez obtenida la varianza, hallamos la desviación estándar:
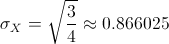





6 comentarios:
Hola,
en el enunciado del problema 3 donde dice función de distribución quiere decir función de densidad verdad?
Buenas:
No, el problema te presenta una distribución que a priori no se define, pero si lees los apartados que debes obtener, el primero, te pide que hagas los cálculos necesarios para que dicha distribución sea una función de densidad.
Un saludo y gracias por tu comentario.
ok, muchas gracias por la aclaración. Es que en muchos textos a la función de distribución acumulada, la llaman simplemente "función de distribución" y de ahí, mi duda en el enunciado, pero ya lo tengo claro.
Gracias!!!
Hola, mis felicitaciones por el blog, un gran aporte. Una duda, en el apartado c se pregunta la P (2 < x < 3), sin embargo, se calcula la P (2 <= x <= 3), por lo que he entendido, supongo que hubo un error al escribir la pregunta no?, o a lo mejor no lo he comprendido, Gracias y nuevamente, mis mas sinceras felicitaciones.
Buenas Ade:
Cuando tratamos de variables aleatorias continuas, los límites no son necesariamente estrictos por el preciso motivo de ser una función continua.
Es decir, si somos severos en la nomenclatura, ¿cuáles serían los límites de acción? ¿1.99 < x < 2.99? o ¿1.9999 < x < 2.9999?.
Como ves, al ser continua la función los límites son infinitesimales, por ende, el cálculo está bien escrito de una manera u otra, no hay error al escribir la pregunta.
Un saludo y gracias por tu comentario.
Gracias por la aclaracion y gracias por este magnifico trabajo.
Un saludo
Publicar un comentario