Ej4. Sea X la cantidad de espacio que ocupa un artículo colocado en una caja de empaque de 1 pie cúbico. La función de distribución de probabilidad de X es:
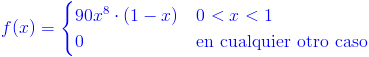
Hallar:
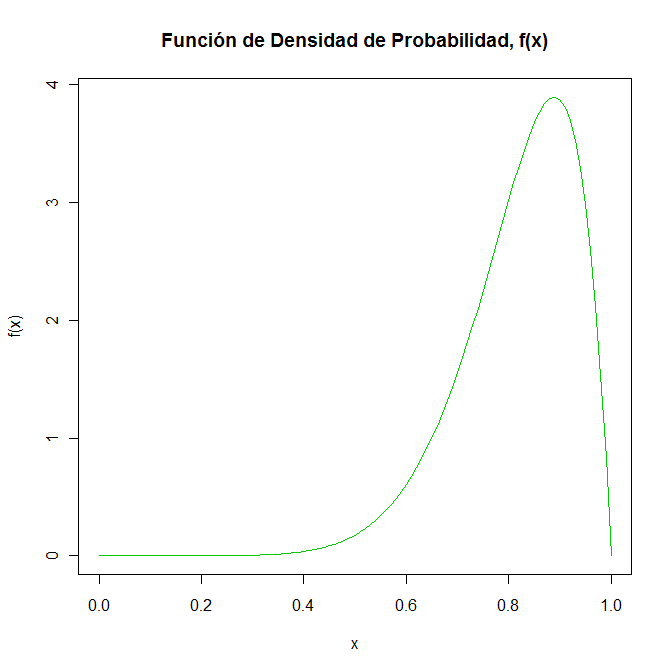
a) Dibuje la función de distribución de probabilidad. Obtenga la función de distribución acumulada y dibújela también.
b) Calcular: P(X ≤ 0.5).
c) Calcular: P(0.25 ≤ X ≤ 0.5) y P(0.25 < X ≤ 0.5).
d) Obtener el valor medio y la desviación estándar.
Apartado a)
Para la representación gráfica de la función de densidad de probabilidad de la variable aleatoria continua X, se utilizará el programa R.
> x=seq(0,1,by=0.01) #Definimos el rango del eje X con un paso de 0.01
> y=90*(x^8)*(1-x) # Función de densidad de probabilidad en el rango X
> plot(x,y,type="l",xlab="x",ylab="f(x)",main="Función de Densidad de Probabilidad, f(x)",col=3)
> x=seq(0,1,by=0.01) #Definimos el rango del eje X con un paso de 0.01
> y=90*(x^8)*(1-x) # Función de densidad de probabilidad en el rango X
> plot(x,y,type="l",xlab="x",ylab="f(x)",main="Función de Densidad de Probabilidad, f(x)",col=3)
Para obtener la función de distribución acumulada, empleamos la siguiente expresión:
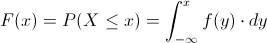
En nuestro caso, el intervalo que tenemos que realizar cálculos es 0 < . X < . 1:
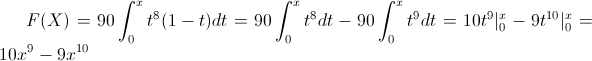
Ya que si x < .0, la función de distribución es 0, y si x > 1, la función de distribución es 1, por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:
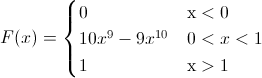
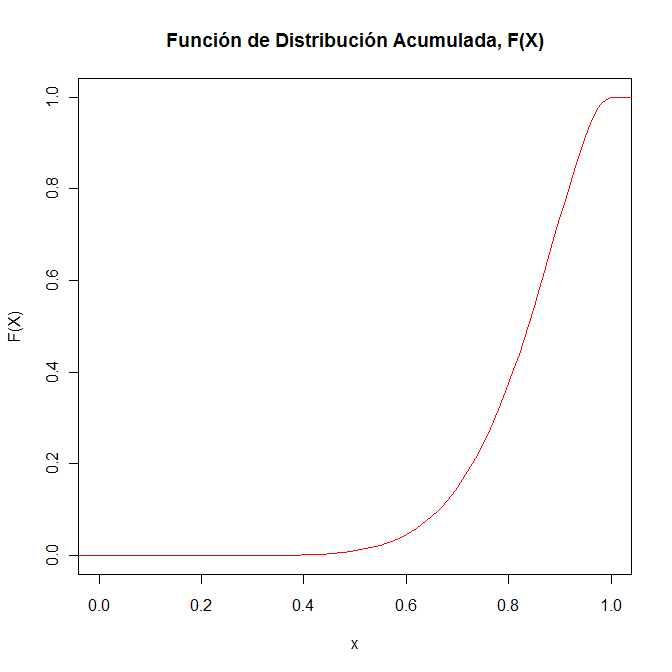
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.
> y1 = 10*x^9 - 9*x^(10) #Función de Distribución Acumulada 0 <. X < . 1
> plot(x,y1,type="l",xlab="x",ylab="F(X)",main="Función de Distribución Acumulada, F(X)",col=2)
> x1 = seq(-1,0)
> y2 =c(0,0)
> lines(x1,y2)
> lines(x1,y2,col=2)
> y3 =c(1,1)
> x2=seq(1,2)
> lines(x2,y3,col=2)
La representación gráfica de la función de distribución acumulada F(X) se muestra en la siguiente figura:
Para calcular la probabilidad de este apartado, empleamos la función de distribución acumulada tal y como se muestra a continuación:
P(X ≤ 0.5) = F(0.5) = 10·0.5⁹ - 9·0.5¹⁰ = 11/1024
Apartado c)
En las variables aleatorias continuas, los límites de las probabilidades no se tienen en cuenta, ya que son variables continuas, por lo tanto:
P(0.25 ≤ X ≤ 0.5) = P(0.25 < X ≤ 0.5) = F(0.5) - F(0.25) = [10·0.5⁹ - 9·0.5¹⁰] - [10·0.25⁹ - 9·0.25¹⁰] ≈ 0.0107
Apartado d)
En este apartado, debemos calcular la esperanza y la desviación estándar de la variable aleatoria continua, X.
Para el cálculo de la esperanza, empleamos la siguiente expresión:
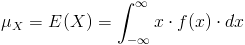
Por lo tanto, la esperanza de X, será:
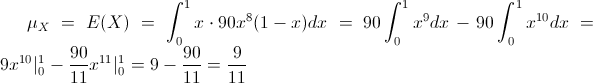
Y para la varianza, se empleará la siguiente expresión:
Var(X) = E(X²) - [E(X)]²
Por lo tanto:
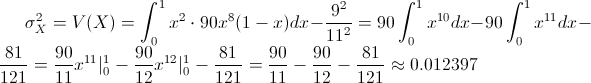
Una vez obtenida la varianza, hallamos la desviación estándar:
σX = √0.012397 ≈ 0.111340





2 comentarios:
Hola que tal, muy buen material de estudio gracias.
Tengo una pregunta en la funcion de distribucion acumulada cuando se dice que 1 si x>1 y 0 x<0, no deberia ser 0 si x>1... gracias de antemano
Buenas:
Si te fijas en la distribución de probabilidad, la función que nos ofrece está definida en el intervalo:
· 0 < x < 1
Matemáticamente, la distribución acumulada es el área de dicha distribución de probabilidad.
Por lo tanto, cuando llegamos al límite superior del intervalo, por fuerza éste debe ser 1.
Ya que se considera todo el área de dicha función de probabilidad.
Si tienes dudas, te puedes fijar en su representación gráfica.
Un saludo y gracias por tu comentario.
Publicar un comentario