Ej5. Sea X una variable aleatoria continua con función de distribución acumulada:
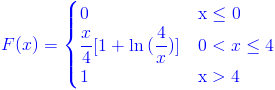
Hallar:
a) Calcular P(X ≤ 1).
b) Calcular P(1 ≤ X ≤ 3).
c) Obtener la función de densidad de probabilidad.
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.
> x = seq(0,4,by=0.1)
> y = (x/4)*(1+log(4/x))
> plot(x,y,type="l",xlab="x",ylab="F(X)",main="Función de Distribución Acumulada, F(X)",col=2)
Apartado a)
Para calcular la probabilidad de este apartado, empleamos la función de distribución acumulada tal y como se muestra a continuación:
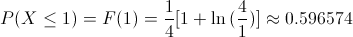
Apartado b)
Se procede igual que en el apartado anterior:
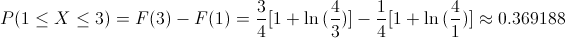
Apartado c)
Para obtener la función de densidad de probabilidad, empleamos la siguiente relación:
F'(x) = f(x)
Por lo tanto, realizamos las derivadas:
La derivada de una constante es cero, por lo que la función de densidad, queda tal y como sigue:
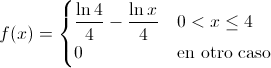
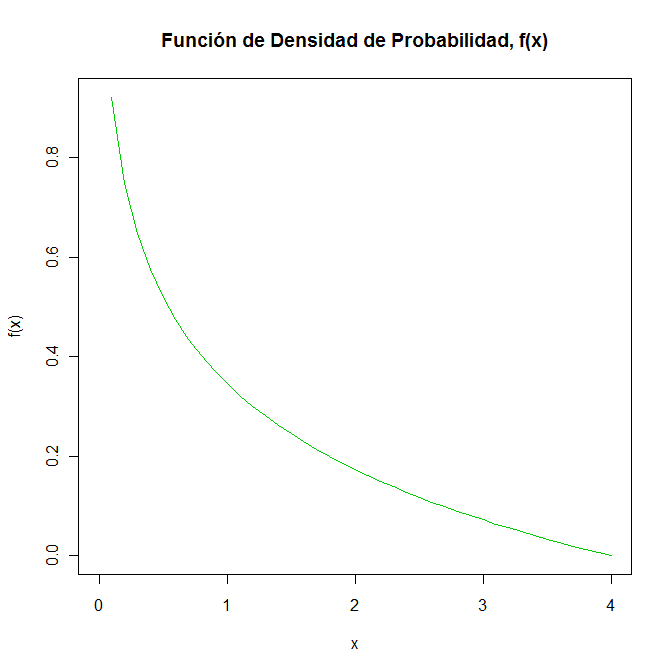
Para la representación gráfica de la función de densidad de probabilidad de la variable aleatoria continua X, se utilizará el programa R.
> y = log(4)/4-(log(x))/4
> plot(x,y,type="l",xlab="x",ylab="f(x)",main="Función de Densidad de Probabilidad, f(x)",col=3)


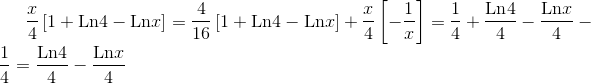




8 comentarios:
Excelente 100% recomendado
¿¿¿¿Y si el intervelo es p(0<X<=4) para el apartado b) ????
Buenas:
Teniendo la función de distribución acumulada, la respuesta es fácil:
· P(0 < X ≤ 4) = F(4) - F(0) = F(4) = (4/4)·[1 + Ln(4/4)] = 1
Era fácil determinar que la probabilidad sería 1 ya que abarca todo el interválo dónde está definida la función.
Un saludo y gracias por tu comentario.
Ola:
Muchisimas gracias por responder!
Me ha servido de gran ayuda pero tengo un problema del mismo tipo que no se como resolver..es decir, si yo realizo el ejercicio de este modo la probabilidad no se si esta del todo bien.
El ejercicio en cuestion es este:
( 0 si x<=3
F(x) ) (x-3)²/9 si 3 < x <= 6
( 1 si x>= 6
si hago para p(1<= X <= 4):
F(4) - F(1) = (4-3)²/9 - 0 =
= (4²-2*3*4-3²)/9 =
= 1/9
solucion = 1/9
sería asi entonces..???
Muchisimas gracias por todo, siempre es de agradecer alguien dispuesto a ayudar.
Buenas:
Para la función de distribución acumulada que tu propones, la solución a la probabailidad requerida es:
· P(1 ≤ X ≤ 4) = F(4) - F(1) = F(4) = (4-3)²/9 = 1/9
Efectivamente, tu solución es la correcta.
· PD: Hola es con h.
Un saludo y gracias por tu comentario.
MUCHAS GRACIAS!!! es estupendo contar con una ayuda tan buena como esta..Muy bien explicado todo!! Excelente!!!
PD: cierto Hola con 'h', metí la pata! jejejej
MAKI EL 4/8 DE LA DERIVADA ESTA MAL, ES 4/16
GRACIAS Y UN SALUDO.
Buenas Antonio:
Tienes razón, ha sido una errata al escribir la expresión ya que el resultado final está bien obtenido.
Un saludo y gracias por el apunte.
Publicar un comentario