Ej9. Sea X el tiempo en horas que funciona adecuadamente la pila de una calculadora solar entre exposiciones a la luz suficientes para recargarla. Suponga que la función de densidad de probabilidad de X está dada por:
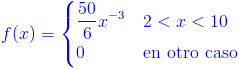
Hallar:
a) Verificar que se trata de una función de densidad de probabilidad válida.
b) Obtener la función de distribución acumulada.
c) Calcular la probabilidad de que la carga de una pila solar seleccionada aleatoriamente dure como mucho, cuatro horas antes de que sea necesario recargarla.
d) Obtener la esperanza, la varianza y la desviación típica de X.
Apartado a)
Para que la función f(x) corresponde a una función de densidad de probabilidad de una variable aleatoria continua, se debe cumplir las siguientes condiciones.
1. f(x) > 0,...para todo x.
2.
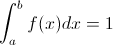
Procedemos:
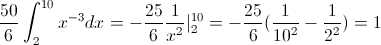
Se cumplen las condiciones por lo que f(x) es una función de densidad de probabilidad legítima de X.
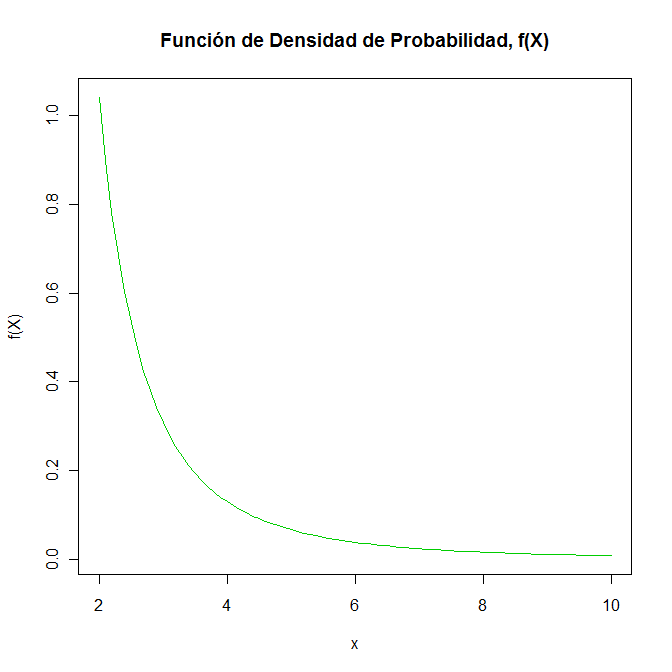
> x = seq(2, 10, by=0.1)
> y = (50/6)*(1/x^3)
> plot(x, y, type="l", xlab="x", ylab="f(X)", main="Función de Densidad de Probabilidad, f(X)", col=3)
Apartado b)
Para obtener la función de distribución acumulada.
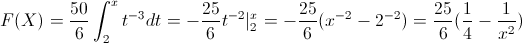
Por lo tanto, la función acumulada quedará:
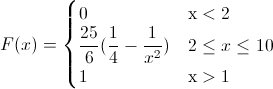
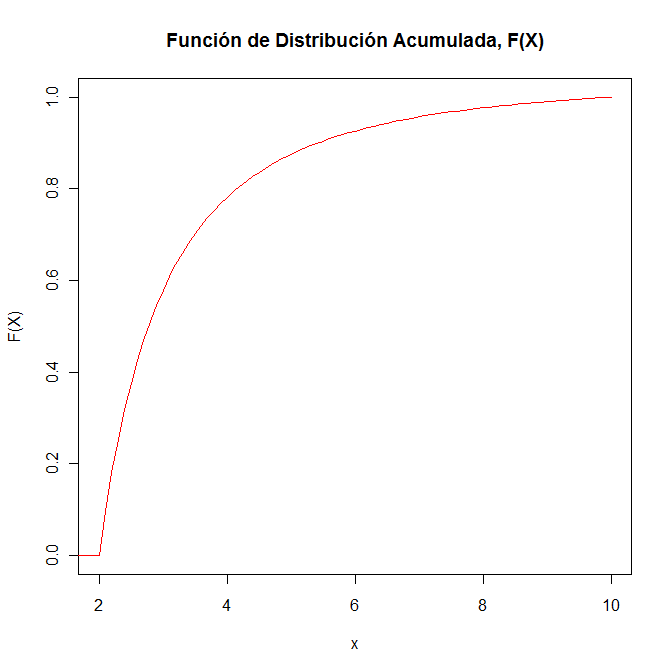
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.
> y1 = (25/6)*(1/4 - 1/x^2)
> plot(x, y1, type="l", xlab="x", ylab="F(X)", main="Función de Distribución Acumulada, F(X)", col=2)
> x2= seq(1,2)
> y2=rep(0,length(x2))
> lines(x2,y2,col=2)
Apartado c)
Para obtener la probabilidad requerida, usamos la función de distribución acumulada del apartado anterior.
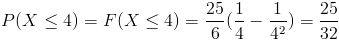
Apartado d)
Para obtener la esperanza de X:
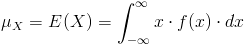
Por lo tanto:
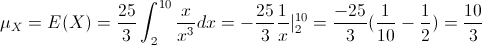
Para la varianza de X:
Var(X) = E(X²) - [E(X)]²
Obtenemos primero:
Var(X) = E(X²) - [E(X)]²
Obtenemos primero:
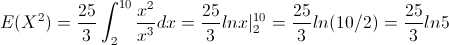
Por lo tanto, la varianza de X será:
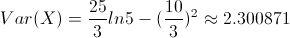
La desviación típica es fácil obtenerla a partir de la varianza de X:
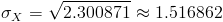





8 comentarios:
Hola Manuel!
Primeramente felicitarte por este Blog que espero que me sea útil de cara mis exámenes.
Tengo una duda en un apartado me dicen que:
En un lab se utilizan 10 gr de Sodio,
Sabiendo que la duración média es de 140 dias.
a) Cuantos dias trasncurriran has que haya desaparecido el 90 %?
Esto haciendo una exponecial inversa me ha dado que son 322 dias.
b)Calcula la probabilidad que habiendo superado los 100 dias, supere los 120.
Esto lo he hecho con una condicionada
c) Realiza los mismos cálculos con el modelo uniforme y calcula sus cuantiles
Aquí es donde me pierdo no se por donde empezar
Si me pudieses echar una mano te lo agradeceria.
Grácias
Buenas:
Voy a ir resolviendo el problema apartado por apartado y explicando los problemas que nos vayamos encontrando.
· X ≡ 'Desaparición del sodio'. X ~ Exp(140) días.
Apartado a)
Debemos obtener los días dado un porcentaje:
· P(X ≤ x) = 0.9
Empleamos la función acumulada de la distribución exponencial:
· 1 - e^(-x/140) = 0.9
Empleamos logaritmo neperiano para despejar la incógnita x y resolvemos:
· x = -140·Ln(0.1) = 322.361913
Por lo tanto, hacen falta 323 días.
Apartado b)
Debemos obtener la siguiente probabilidad:
· P(X > 100+20 | X > 100)
Un aspecto siempre a recordar de la distribución exponencial es que no posee memoria, por lo tanto:
· P(X > 100+20 | X > 100) = P(X > 20) = 1 - P(X ≤ 20)
Volvemos a emplear la función acumulada de dicha distribución y resolvemos:
· P(X > 100+20 | X > 100) = 1 - P(X ≤ 20) = 1 - [1 - e^(-20/140)] ≈ 0.866878
Apartado c)
Realmente este apartado es un poco extraño, ya que se juega con la relación entre cierta distribución uniforme y la exponencial.
Intentare explicarlo lo más claro posible, cuando una variable continua sigue una distribución uniforme que está configurada de la siguiente manera: X ~ U(0, 1)
Existe relación entre dicha distribución y la exponencial de la siguiente forma:
· x = -β·Ln(1 - u)
Donde:
· x ≡ Variable de la distribución exponencial que deseamos a obtener. En nuestro problema, sería el tiempo transcurrido en desaparecer el Sodio.
· β ≡ Tiempo medio de la variable de distribución exponencial. En nuestro caso, 140 días.
· u ≡ Valor aleatorio que sigue una distribución uniforme del tipo U(0, 1). Esto quiere decir que los valores que podrá tomar están comprendidos entre: 0 < u < 1.
Entonces, teniendo en cuenta dicha teoría, para el primer apartado, la probabilidad del 90%, sustituimos en la expresión anterior:
· x = -β·Ln(1 - u) = -140·Ln(1 - 0.9) = 322.361913
Como podemos observar, ambos valores coinciden y no es de extrañar, ya que si nos fijamos bien, cuando resolvemos por la distribución exponencial se asume de por sí, que se está empleando una distribución uniforme de las características mencionadas.
Con respecto a los cuartiles, son tres: 0.25, 0.5 y 0.75.
Empleando la misma expresión que la anterior pero teniendo e cuenta que para los cuartiles, por definición, debemos emplear la inversa, obtenemos:
· Primer cuartil: β·Ln(4/3) = 140·Ln(4/3) ≈ 40.275490
· Segundo cuartil: β·Ln(2) = 140·Ln(2) ≈ 97.040605
· Tercer cuartil: β·Ln(4) = 140·Ln(4) ≈ 194.081211
Un saludo.
Grácias mis resultados son los mismos, excepto para los cuartiles que en vez de multiplicar beta, la he dividido.
NOTA: mediante el cálculo de cuantiles mediante R me da mi mismo resultado.
Una cosa: La relación entre Exponencial y Uniforme de donde la ha obtenido?
Yo explico mis intenciones de cara al ultimo apartado:
Tengo que encontrar los valores a y b de la uniforme.
solo con la media.
Entonces a partir de
E(X)= (a+b)/2
de var(x)= (b-a)^2/12
y de la integral de var(x)entre[a,b] QUE NO SE DEFINIRLA encuentro parametros a y b para luego hallar X
No se si me explico!
Como lo he dicho estaria bién??
Si es que si, como seria esta integral?
Grácias!
Buenas:
La relación entre la exponencial y la distribución uniforme se da cuando la distribución uniforme tiene de parámetros: a = 0 y b = 1.
Entonces se dice que es una distribución uniforme estándar. Y se puede hacer un cambio de variable hacia una distribución exponencial o hacia una distribución beta.
En nuestro caso, hacia la distribución exponencial es tal y como te he indicado en el comentario anterior.
Con respecto a los cuantiles. Ten en cuenta, que R para obtener dichos parámetros hace la transformación a la exponencial. Y si te fijas bien, la distribución en R de la exponencial es ligeramente distinta a cómo yo la defino. El parámetro medio para R es la inversa del que yo defino:
· λ = 1/β
Donde:
· λ ≡ Parámetro medio para R.
· β ≡ Parámetro medio para nosotros.
¡Ojo! Ambos son iguales, sólo que si te fijas en la distribución en R, el parámetro medio lo transforman a la inversa del nuestro.
Y por último, encontrar los parámetros a y b que definen la distribución uniforme con la media, tendrías una ecuación con dos incógnitas. Al menos te deberían dar la varianza.
No se si al desarrollar la media o la varianza mediante la distribución de densidad podría a obtenerse algo, aunque lo dudo, sobre todo porque sería algo muy rebuscado y poco práctico y lo que es más importante: nada útil.
Un saludo.
Ok!
Grácias.
Solo un apunte, tendria 2 ecuaciones dos incognitas, porque con el modelo exponencial donde Var(x)=E(x)^2 donde hallaría la var(x).
En mi caso elevando al cuadrado 140.
Que me da una varianza de 19600.
Resuelvo y hallo los valores de a y b.
Pero a me da negativa, y eso no creo que sea posible no??
Grácias y perdona molestarte un domingo de ramos.
Buenas:
Los parámetros de la distribución uniforme están definidos entre el rango:
· -∞ < a, b < ∞
Desde un punto matemático, sólo estamos resolviendo la integral que encierra dichos parámetros. pero desde un punto de vista estadístico, por convenio la probabilidad está comprendida entre el siguiente rango:
· 0 < p < 1
Yo no veo muy claro la relación directa de obtener los parámetros de la uniforme igualando las medias de ambas distribuciones por que sí.
Más bien sigo manteniendo la teoría de que está hablando de la distribución uniforme estándar que sí mantiene una relación directa de cambio de variable con la exponencial.
Un saludo y gracias por tu comentario.
Por favor quisiera saber esto: en el ejercicio me dan una fdp, y me piden la variaza de otra, es decir supongo
f(x) = cx*2
y me piden la esperanza de
E[3X*2-2X+3]
CÓMO LO HAGO?
Buenas Lina:
Lo primero que deberás averiguar es el valor de c para que la función dada sea una función de densidad.
Una vez lo obtengas, deberás hallar la esperanza, sustituyendo tu fdp con la expresión dada.
Un saludo.
Publicar un comentario