Ej8. Considere la siguiente función de densidad de probabilidad de la variable aleatoria X:
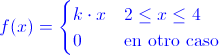
Hallar:
a) Obtener el valor de k para que f(x) sea una función de densidad de probabilidad de X legítima.
b) Obtener la función de distribución acumulada.
c) Calcular la siguiente probabilidad: P(1 ≤ X ≤ 4).
d) Obtener la esperanza, la varianza y la desviación típica de X.
Apartado a)
Para que la función f(x) corresponde a una función de densidad de probabilidad de una variable aleatoria continua, se debe cumplir las siguientes condiciones:
Para que f(x) sea una función de densidad de probabilidad, se deben satisfacer:
1. f(x) > 0,...para todo x.
2.
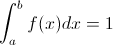
Procedemos:
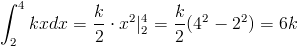
Se debe cumplir: 6k = 1, por lo tanto, el valor de k es: k = 1/6.
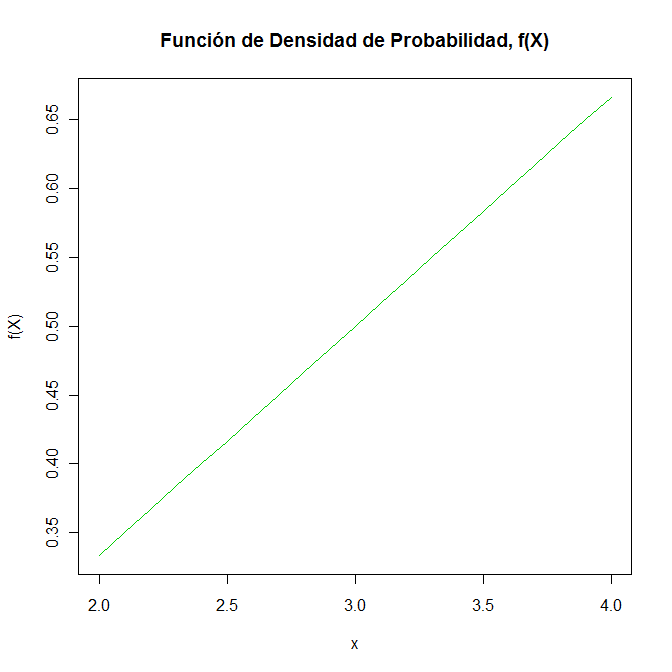
La función de densidad de probabilidad de X quedará:
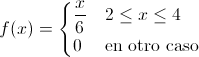
> x = seq(2, 4, by=0.1)
> y = (1/6)*x
> plot(x, y, type="l", xlab="x", ylab="f(X)", main="Función de Densidad de Probabilidad, f(X)", col=3)
Apartado b)
Para obtener la función de distribución acumulada.
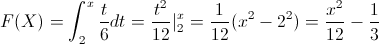
Por lo tanto, la función acumulada quedará:
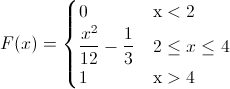
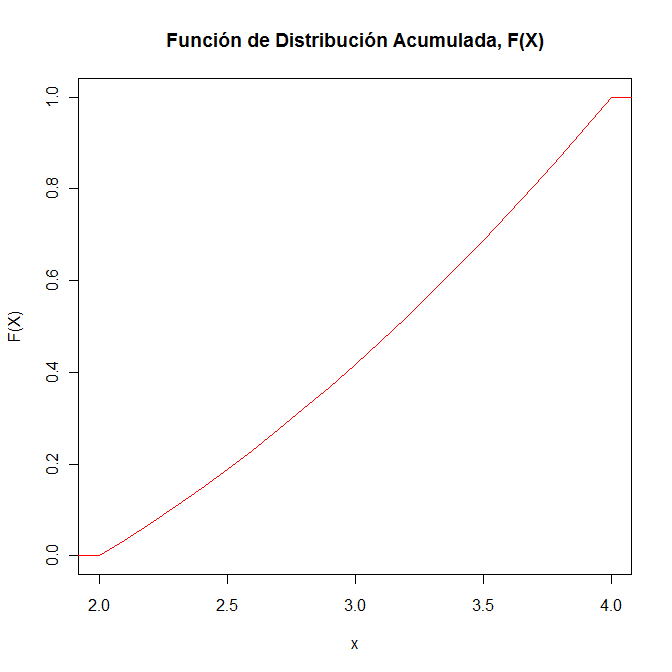
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.
> x = seq(2, 4)
> y = (x^2/12)-(1/3)
> plot(x, y, type="l", xlab="x", ylab="F(X)", main="Función de Distribución Acumulada, F(X)", col=2)
> x1 = seq(1, 2)
> y1 = rep(0, length(x1))
> lines(x1, y1, col=2)
> x2 = seq(4, 5)
> y2 = rep(1, length(x2))
> lines(x2, y2, col=2)
Apartado c)
Para obtener la probabilidad requerida, usamos la función de distribución acumulada del apartado anterior.
P(1 ≤ X ≤ 4) = F(4) - F(1) = 16/12 - 1/3 - 0 = 1
Esto es así ya que estamos justamente en el límite de la curva de la distribución de probabilidad acumulada.
Apartado d)
Para obtener la esperanza de X:
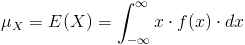
Por lo tanto:
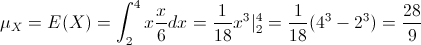
Para la varianza de X:
Var(X) = E(X²) - [E(X)]²
Obtenemos primero:
Var(X) = E(X²) - [E(X)]²
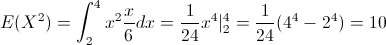
Por lo tanto, la varianza de X será:
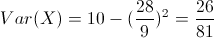
La desviación típica es fácil obtenerla a partir de la varianza de X:
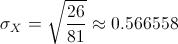





3 comentarios:
¿En el apartado c) F(1) no sería cero?porque para x<2 F(x)=0
yo tambien pienso que F(1) es 0. supongo que se le habra pasado por alto
Buenas:
Es cierto, F(1) es cero por la propia definición de los límites en la distribución acumulada de probabilidad.
Gracias por el dato, realmente se me había pasado.
Publicar un comentario