Ej7. Algunos plásticos de automóviles desechados se pueden separar de ellos y degradar para recuperar los componentes químicos. El mayor éxito ha sido el procesamiento del acojinamiento flexible de poliuretano de esos vehículos. Sea X la cantidad de ese material en libras por automóvil. Suponga que la función de densidad de probabilidad de X está dada por:
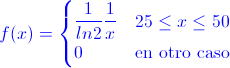
Hallar:
a) Verificar que dicha función de densidad de probabilidad corresponde a una variable aleatoria continua.
b) En el supuesto que la función f(x) describe adecuadamente el comportamiento de la variable aleatoria X, calcule la probabilidad de que un automóvil seleccionado al azar contenga entre 30 y 40 lb de acojinamiento de poliuretano.
c) Obtenga la media, la varianza y la desviación típica de X.
Apartado a)
Para verificar que la función f(x) corresponde a una función de densidad de probabilidad de una variable aleatoria continua, se debe cumplir las siguientes condiciones:
Para que f(x) sea una función de densidad de probabilidad, se deben satisfacer:
1. f(x) > 0,...para todo x.
2.
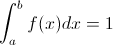
Procedemos a comprobarlo:
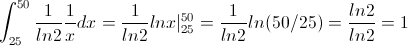
Como podemos observar, cumple las dos condiciones, por lo que podemos decir que la función f(x) es una función de densidad de probabilidad para la variable aleatoria X dada.
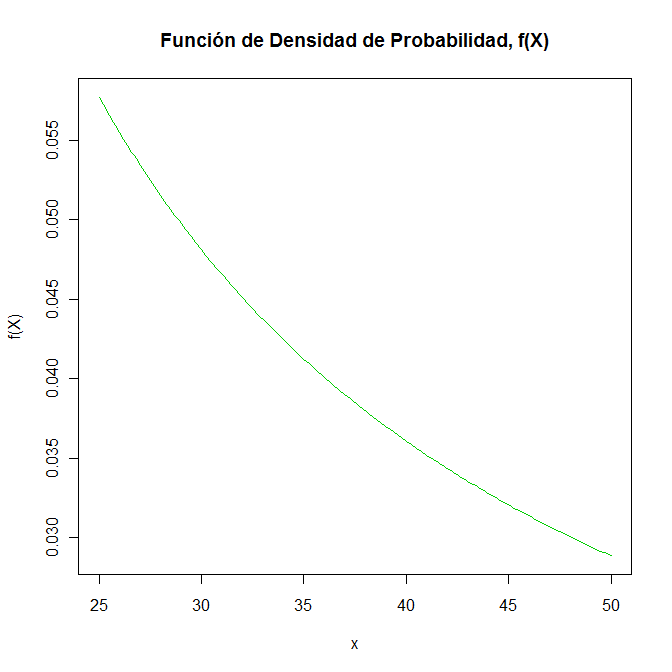
Para la representación gráfica de la función de densidad de probabilidad de la variable aleatoria continua X, se utilizará el programa R.
> x = seq(25, 50, by=0.1)
> y = (1/log(2))*(1/x)
> plot(x, y, type="l", xlab="x", ylab="f(X)", main="Función de Densidad de Probabilidad, f(X)", col=3)
Apartado b)
Para obtener la probabilidad requerida, vamos, previamente, a obtener la función de distribución acumulada.
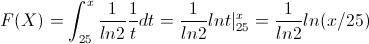
Por lo tanto, la función acumulada quedará:
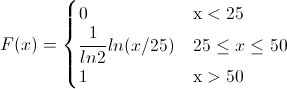
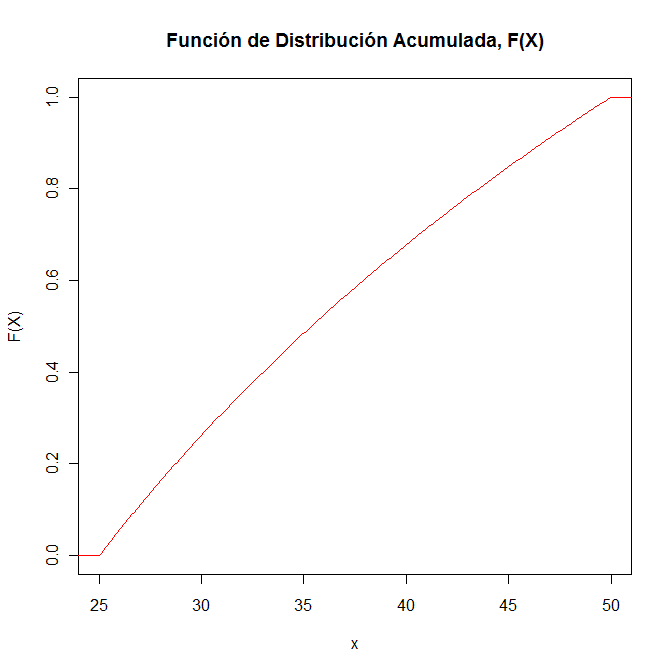
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.
> x = seq(25, 50, by=0.1)
> y = (1/log(2))*(log(x/25))
> plot(x, y, type="l", xlab="x", ylab="F(X)", main="Función de Distribución Acumulada, F(X)", col=2)
> x1 = seq(50, 53)
> y1 = rep(1, 4)
> lines(x1, y1, col=2)
> x2 = seq(23, 25)
> y2 = rep(0, 3)
> lines(x2, y2, col=2)
Ahora, calculamos la probabilidad requerida:
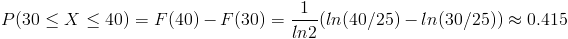
Apartado c)
Para obtener la esperanza de X:
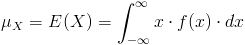
Por lo tanto:
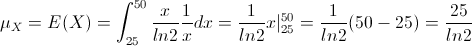
Para la varianza de X:
Var(X) = E(X²) - [E(X)]²
Obtenemos primero:
Var(X) = E(X²) - [E(X)]²
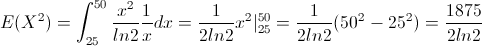
Por lo tanto, la varianza de X será:
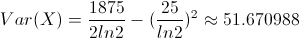
La desviación típica es fácil obtenerla a partir de la varianza de X:
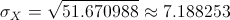





0 comentarios:
Publicar un comentario