Problema 6: VAC

Ej6. Sea X la duración, en minutos, de una conversación telefónica de larga distancia. Se supone que la función de densidad de probabilidad de X está determinada por:

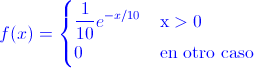
Hallar:

a) Verificar que dicha función de densidad de probabilidad corresponde a una variable aleatoria continua.

b) En el supuesto que la función f(x) describe adecuadamente el comportamiento de la variable aleatoria X, calcule la probabilidad de que una llamada seleccionada aleatoriamente dure cuando mucho 7 minutos. Calcule también que dure al menos 7 minutos y obtenga la probabilidad de que dure exactamente 7 minutos.

Apartado a)

Para verificar que la función f(x) corresponde a una función de densidad de probabilidad de una variable aleatoria continua, se debe cumplir las siguientes condiciones:

Para que f(x) sea una función de densidad de probabilidad, se deben satisfacer:

1. f(x) > 0,...para todo x.

2.

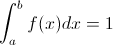
Procedemos a comprobarlo:

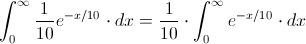
Realizamos el cambio de variable:

· t = -x/10
· dt = - dx/10

Por lo tanto:

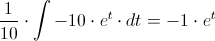
Deshacemos el cambio de variable y resolvemos:

Como podemos observar, cumple las dos condiciones, por lo que podemos decir que la función f(x) es una función de densidad de probabilidad para la variable aleatoria X dada.

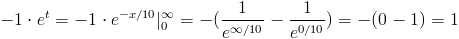
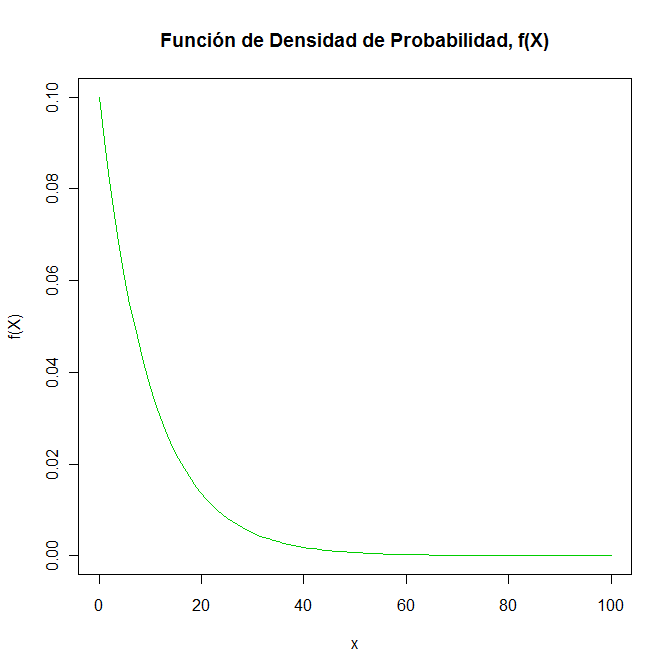
Para la representación gráfica de la función de densidad de probabilidad de la variable aleatoria continua X, se utilizará el programa R.

> x = seq(0, 100, by=1)
> y = (1/10)*exp(-x/10)
> plot(x, y, type="l", xlab="x", ylab="f(X)", main="Función de Densidad de Probabilidad, f(X)", col=3)

Apartado b)

Para obtener las probabilidades requeridas, vamos, previamente, a obtener la función de distribución acumulada.

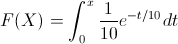
Realizando el cambio de variable similar al mostrado en el apartado anterior, obtenemos, finalmente:

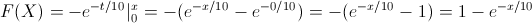
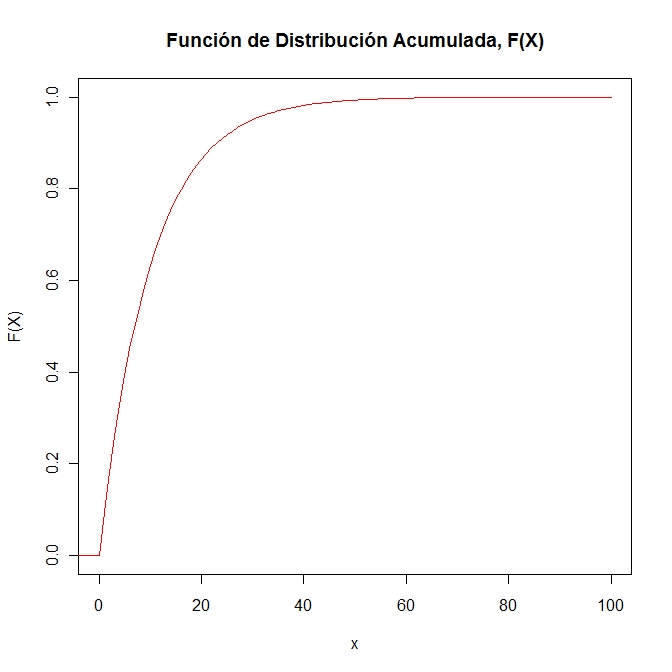
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.

> x = seq(0, 100, by=1)
> y = (1/10)*exp(-x/10)
> plot(x, y, type="l", xlab="x", ylab="F(X)", main="Función de Distribución Acumulada, F(X)", col=2)
> x1 = seq(-1, 0)
> y2 = rep(0, 11)
> lines(x1, y2, col=2)

Ahora, calculamos las probabilidades requeridas:

· P(X ≤ 7) = 1 - e^-7/10 ≈ 0.503415

· P(X ≥ 7) 1 - P(X ≤ 7) = 1 - (1 - e^-7/10) ≈ 0.496585

· P(X = 7) = 0

Es cero ya que un valor concreto no corresponde a una variable aleatoria continua, matemáticamente es fácil su demostración, la derivada de una constante es cero.

Y geométricamente, también es fácil corroborarlo, ya que el área encerrada bajo la curva de la función de distribución acumulada de un punto concreto es cero.