Problema10: VAC

Ej10. Sea una variable aleatoria continua X que indica el diámetro de un agujero perforado en una hoja de metal. Los datos históricos muestran que la distribución de X puede ser modelado por una función de densidad de probabilidad:

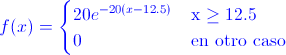
Hallar:

a) Verificar que se trata de una función de densidad de probabilidad válida.

b) Obtener la función de distribución acumulada.

c) Calcular la probabilidad P(12.5 ≤ X ≤ 12.6).


Apartado a)

Para que la función f(x) corresponde a una función de densidad de probabilidad de una variable aleatoria continua, se debe cumplir las siguientes condiciones.

1. f(x) > 0,...para todo x.

2.

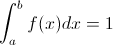
Procedemos:

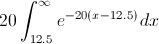
Hacemos un cambio de variable:

· t = -20(x - 12.5)
· dt = -20dx

Aplicamos el cambio de variable:

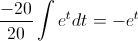
Deshacemos el cambio de variable y resolvemos:

Se cumplen las condiciones por lo que f(x) es una función de densidad de probabilidad legítima de X.

Para la representación gráfica de la función de densidad de probabilidad de la variable aleatoria continua X, se utilizará el programa R.

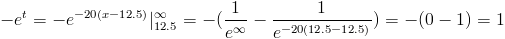
> x <- seq(12.5, 13, by=0.001) > y = 20*exp(-20*(x-12.5))
> plot(x, y, type="l", col=3, xlab="x", ylab="f(x)", main="Función de Densidad de Probabilidad")

Apartado b)

Para obtener la función de distribución acumulada.

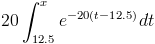
Realizamos un cambio de variable del apartado anterior y resolvemos:

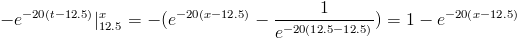
Por lo tanto, la función acumulada quedará:

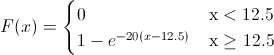
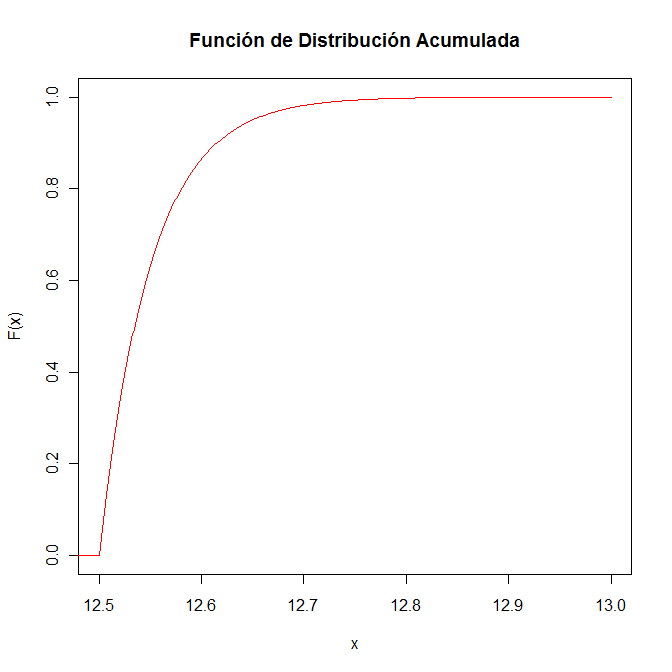
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.

> y1 = 1-exp(-20*(x-12.5))
> plot(x,y1,type="l",col=2,xlab="x",ylab="F(x)",main="Función de Distribución Acumulada")
> x1=seq(12,12.5,by=0.5)
> y2=rep(0,length(x1))
> lines(x1,y2,col=2)

Apartado c)

Para obtener la probabilidad requerida, usamos la función de distribución acumulada del apartado anterior.

P(12.5 ≤ X ≤ 12.6) = F(12.6) - F(12.5) = (1 - e^{-20(12.6-12.5)}) - (1 - e^{-20(12.5-12.5)}) = 1 - e^-2 ≈ 0.864665