Problema2: t Student

Ej2. Calcule los siguientes valores de la distribución t Student:

a) Con v = 25, P(-t ≤ T ≤ t) = 0.90.

b) Con v = 25, P(-t ≤ T ≤ t) = 0.95.

c) Con v = 15, P(T ≥ t) = 0.05.

d) Con v = 20, P(T ≥ t) = 0.10.

e) Con v = 16, P(T ≤ -t) = 0.05.

f) Con v = 30, P(T ≤ -t) = 0.10.



Apartado a)

Hay que tener en cuenta que las tablas disponibles en Aqueronte presentan el área de cola, por lo tanto:

1 - 0.90 = 0.1

Desarrollamos la probabilidad requerida:

P(-t ≤ T ≤ t) = Φ(t) - (-Φ(t)) = 2Φ(t) = 0.1

Por lo tanto:

Φ(t) = 0.1/2 = 0.05

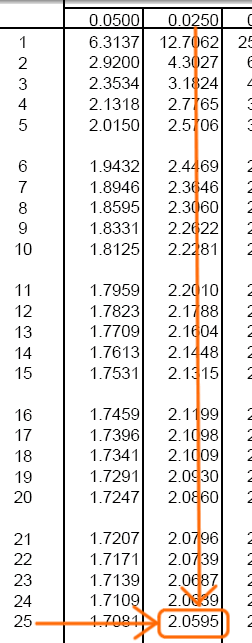
Ahora, disponemos del área de cola (0.05) y los grados de libertad (25), por lo que buscamos en la tabla el valor requerido:

Por lo tanto, la solución a este apartado es: 1.7081.


Apartado b)

Actuamos de forma similar al apartado anterior, hay que tener en cuenta que las tablas disponibles en Aqueronte presentan el área de cola, por lo tanto:

1 - 0.95 = 0.05

Desarrollamos la probabilidad requerida:

P(-t ≤ T ≤ t) = 2Φ(t) = 0.05

Por lo tanto:

Φ(t) = 0.05/2 = 0.025

Ahora, disponemos del área de cola (0.025) y los grados de libertad (25), por lo que buscamos en la tabla el valor requerido:

Por lo tanto, la solución a este apartado es: 2.0595.


Apartado c)

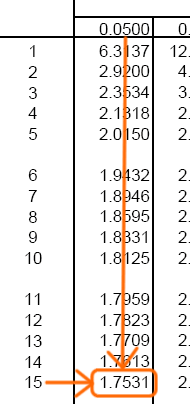
Disponemos del área de cola (0.05) y los grados de libertad (15), por lo que buscamos en la tabla el valor requerido:

Por lo tanto, la solución a este apartado es: 1.7531.


Apartado d)

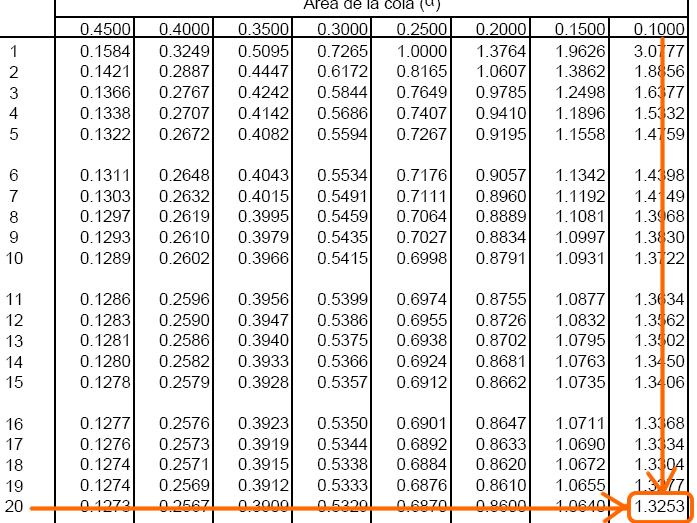
Disponemos del área de cola (0.10) y los grados de libertad (20), por lo que buscamos en la tabla el valor requerido:

Por lo tanto, la solución a este apartado es: 1.3253.

Apartado e)

Operamos en la probabilidad dada:

P(T ≤ -t) = P(T ≥ t) = 0.05

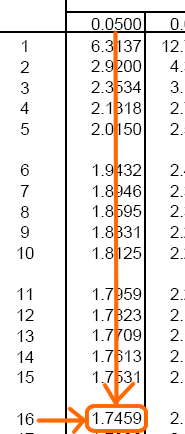
Disponemos del área de cola (0.05) y los grados de libertad (16), por lo que buscamos en la tabla el valor requerido:

Por lo tanto, la solución a este apartado es: 1.7459.


Apartado f)

Al igual que en el apartado anterior, operamos en la probabilidad dada:

P(T ≤ -t) = P(T ≥ t) = 0.10

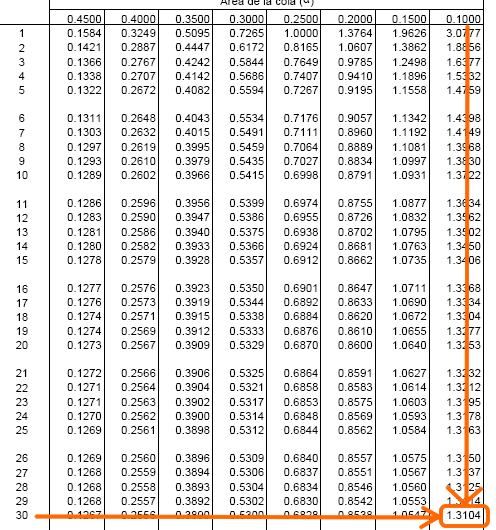
Disponemos del área de cola (0.10) y los grados de libertad (30), por lo que buscamos en la tabla el valor requerido:

Por lo tanto, la solución a este apartado es: 1.3104.