Ej12. Halla un intervalo de confianza del 99% para la varianza de una población normal, de la que se ha extraído la siguiente muestra:1.19. 1.23. 1.18. 1.21. 1.27. 1.17. 1.15. 1.14 1.19 1.20
En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.
Para obtener la media:
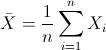
Por lo tanto:
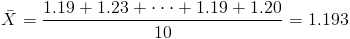
Para obtener la cuasi varianza:
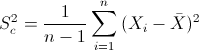
Por lo tanto:
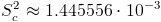
En este problema nos pide realizar un intervalo de confianza para la varianza con la media desconocida:
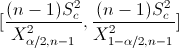
Para una confianza del 99%, obtenemos α:
100(1 - α) = 99
Despejamos el parámetro que nos interesa: α = 0.01. El siguiente paso es obtener los valores de:
· 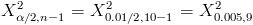
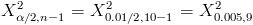
·
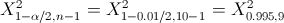
Buscamos el valor en la tabla ji-cuadrada, y obtenemos: 23.59 y 1.73 respectivamente.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 99%, simplemente, sustituimos valores:
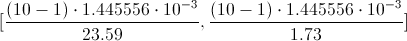
[5.515050·10-4, 7.520233·10-3]





4 comentarios:
¿Faltaría parte del enunciado?
Muchas gracias por el blog.
Buenas:
No falta nada, el enunciad está completo, obtener un intervalo de confianza del 99% para la varianza de una población normal dada una muestra.
Un saludo.
No se trataria de un intervalo de confianza para la varianza con la media CONOCIDA (en vez de desconocida??) ya que al poder calcularla con los datos del enunciado seria conocida, pregunto.
Publicar un comentario