Ej11. Un ingeniero de control de calidad midió el espesor de la pared de 25 botellas de vidrio de dos litros. La media muestral es 4.05 mm, mientras que la cuasi desviación estándar muestral es de 0.08 mm.
Encuentra un intervalo de confianza del 90% para la media del espesor de la pared de las botellas.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· Media: X1 = 4.05.
· Cuasi desviación estándar: Sc = 0.08.
· Tamaño de la muestra: n = 25.
En este problema nos pide realizar un intervalo de confianza para la media con varianza desconocida y el tamaño de la muestra es menor que 30:
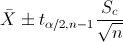
Para una confianza del 90%, obtenemos α:
100(1 - α) = 90
Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la t:
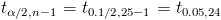
Buscamos el valor en la tabla t-Student, y obtenemos: 1.7109.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 90%, simplemente, sustituimos valores:
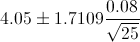
El intervalo de confianza bilateral al 90% es:
[4.022626, 4.077374]





3 comentarios:
Por que utilizas t y no z para el nivel de significancia?
Buenas:
Porque para encontrar un intervalo de confianza para la media con la varianza desconocida y el tamaño de la muestra menor de 30 elementos, las tablas dicen que debemos emplear el parámetro t en vez del z.
Un saludo y gracias por tu comentario.
como que varianza desconocida si se conoce la desviacion, eso sale con distribucion normal!!
Publicar un comentario