Ej10. Una máquina produce las varillas de metal utilizadas en el sistema de suspensión de un automóvil. Se toma de una muestra aleatoria de 15 varillas y se mide el diámetro, obteniéndose los datos siguientes:
| 8.24. | 8.21. | 8.23. | 8.25. | 8.26. | 8.20. | 8.23. | 8.26 |
| 8.19 | 8.23 | 8.20 | 8.28 | 8.24 | 8.25 | 8.24 |
Construya un intervalo de confianza bilateral del 95% para la media del diámetro de la varilla.
En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.
Para obtener la media:
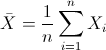
Por lo tanto:
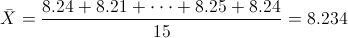
Para obtener la cuasi varianza:
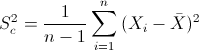
Por lo tanto:
En este problema nos pide realizar un intervalo de confianza para la media con varianza desconocida y el tamaño de la muestra es menor que 30:
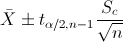
Para una confianza del 95%, obtenemos α:
100(1 - α) = 95
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la t:
Buscamos el valor en la tabla t-Student, y obtenemos: 2.1448.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:
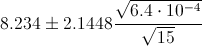
El intervalo de confianza bilateral al 95% es:
[8.219990, 8.248010]





4 comentarios:
Tengo una duda, el estadistico (no se si se llama asi), no seria Z?
Un saludo
Fallo mio, me habia ido al apartado general. los siento.
¿Faltaría parte del enunciado?
Muchas gracias por el blog.
Buenas:
Bueno, faltaba de estar en color azul dicha parte: Construya un intervalo de confianza bilateral del 95% para la media del diámetro de la varilla.
Pero el enunciado en sí estaba completo, aún así, ya está subsanado.
Un saludo.
Publicar un comentario