Ej9. Se estudia las tasas de combustión de dos propelentes sólidos utilizados en los sistemas de escape de emergencia de aeroplanos. Se sabe que las tasas de combustión de dos propelentes tienen la misma desviación estándar de valor 3 cm/s.
Se prueban dos muestras aleatorias de 20 especímenes para cada muestra aleatoria. Las medias muestrales de las tasas de combustión son 18 cm/s y 24 cm/s.
Construya un intervalo de confianza bilateral del 99% para la diferencia entre las medias de las tasas de combustión. ¿Qué tamaño de muestra debe utilizarse en cada población si se desea que el error en la estimación de la diferencia entre las medias de las tasas de combustión sea menor que 4 cm/s con una confianza del 99%?
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· Propelente 1: X1 = 18, σ1 = 3, n1 = 20.
· Propelente 2: X2 = 24, σ2 = 3, n2 = 20.
En este problema nos pide realizar un intervalo de confianza para la diferencia entre las medias con varianzas conocidas:
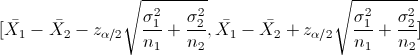
Para una confianza del 99%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.01. El siguiente paso es obtener el valor de la z:
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.495, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:
..2.57...........Z..... ..2.58
0.4949.....0.495.. .0.4951
De donde:
2.57 - 2.58.---> 0.4949 - 0.4951
2.57 - Z.---> 0.4949 - 0.495
Calculamos:
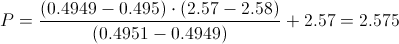
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 99%, simplemente, sustituimos valores:
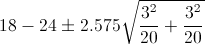
El intervalo de confianza bilateral al 99% es:
Para obtener el tamaño de la muestra en en cada población para un error menor de 4:
Suponiendo que ambas poblaciones tienen el mismo tamaño:
Despejamos n y sustituimos valores para obtener el tamaño de n mínimo:
Como el tamaño de la muestra debe ser un número entero, en este caso 8, y para que el error sea menos de 4 cm/s, el tamaño de la muestra debe ser mayor o igual que 8.

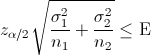
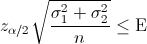
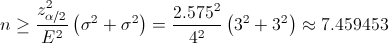




8 comentarios:
Como el enunciado nos dice que el error debe de ser menor que 4,¿no deberiamos escoger el entero mas cercano?
Muchisimas grasias por el blog es una salvacion!!
no seria 7 en vez de 8??????
Buenas:
Según está expuesto sí, tienes razón, pero el fallo (tremendo) ha sido mio, al escribir las ecuaciones en LaTeX me ha jugado una mala pasada y he puesto el signo de la desigualdad al contrario.
Te explico, el error máximo admisible es la expresión que corresponda a cada distribución.
Por ello, si en el enunciado del problema nos dicen que no se puede superar un determinado error, por supuesto dicho error no puede nunca ser mayor que el máximo admisible que hemos tolerado (la expresión matemática de cada distribución).
Y por lo que veo, en los demás problemas también me he equivocado, por lo que me pongo manos a la obra para arreglarlo.
Un saludo y muchísimas gracias por tu comentario.
la formula del error creo que esta mal,porque de desviacion estandar del 2ºelemento esta elevado al cuboy y deberia estar elevada al cuadrado,por lo tanto el resultado en vez de ser n>=8 en el caso que estoy resolviendo es n>= 30.me gustaria que alguien respondiese mi duda,ya que no se si es un fallo mio o una erata del ejercicio.
un saludo.
Buenas:
Lo siento muchísimo pero ha vuelto a ser un error mio al utilizar LaTeX en su momento, para cambiar la expresión, parece ser, que volví a escribirla mal y evidentemente, no la repasé.
El problema estaba al despejar, la expresión resultante no había por donde cogerla, ahora está bien. Eso si, el resultado estaba correcto.
Un saludo y gracias por la anotación.
Buenas. Antes de nada, excelente blog, mi más sincera enhorabuena.
Ya, a lo importante. ¿No estaría mal el intervalo de confianza bilateral al 99%? Me refiero al orden. Creo que debería ser el -8 a la izquierda y el -3 a la derecha. Simplemente por orden de magnitud de ambos valores. De nuevo, felicidades por el blog. Un saludo.
Buenas:
Tienes razón, es más si aplicas la fórmula para obtener el intervalo, ésta te muestra los datos en la dirección correcta.
Por lo que veo en los comentarios, cuando tuvimos el problema grave con las expresiones en LaTeX, éste problema en concreto se ha llevado la peor parte.
Ya está subsanado, muchas gracias por el apunte.
Un saludo.
Entonces, después de todos los errores que detectaron los comentarios anteriores, ya está corregido?
Publicar un comentario