Problema8: Estimación y Pruebas de Hipótesis

Ej8. Se utilizan dos máquinas para llenar botellas de plástico con detergentes para máquinas lavaplatos. Se sabe que la desviación estándar del volumen de llenado son 0.1 u.v. y 0.15 u.v., respectivamente.

Se toman dos muestras aleatorias, 30 botellas de la máquina 1 y 45 botellas de la máquina 2. Los volúmenes promedio de llenado son 30.87 u.v. y 30.68 u.v.

Construye un intervalo de confianza bilateral del 90% y del 95% para la diferencia entre las medias del volumen de llenado.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· Máquina 1: X₁ = 30.87, σ₁ = 0.1, n₁ = 30.
· Máquina 2: X₂ = 30.68, σ₂ = 0.15, n₂ = 45.

En este problema nos pide realizar un intervalo de confianza para la diferencia entre las medias con varianzas conocidas:

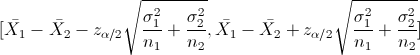
Para un Intervalo del 90%.

Para un 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la z:

z_α/2 = z_0.1/2 = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.45, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..1.64...........Z..... ..1.65
0.4495.....0.45.. .0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z.-> 0.4495 - 0.45

Calculamos:

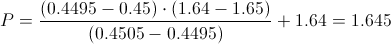
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 90%, simplemente, sustituimos valores:

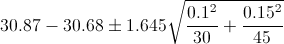
El intervalo de confianza bilateral al 90% es:

[0.142513, 0.237487]

Para un Intervalo del 95%.

Para un 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:

z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.45, y dicho valor es z = 1.96.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:

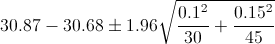
El intervalo de confianza bilateral al 95% es:

[0.133420, 0.246580]

Como podemos observar, si la probabilidad se aumenta, crece la amplitud del intervalo.