Ej7. Se sabe que la duración en horas, de un foco de 75 W., tiene una distribución aproximadamente normal, con una desviación estándar de 25 horas. Se toma una muestra aleatoria de 20 focos, la cual resulta tener un promedio de 1014 horas.
Construir un intervalo de confianza bilateral del 95% para la media de la duración.
¿Qué tamaño de la muestra debe utilizarse si se desea una confianza del 95% en que el error en la estimación de la duración media sea menor que 5 horas?
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· Desviación estándar: σ = 25.
· Media: μ = 1014.
· Tamaño de la muestra: n = 20.
En este problema nos pide realizar un intervalo de confianza para la media con varianza conocida:
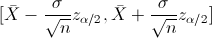
Para un 95%, obtenemos α:
100(1 - α) = 95
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:
zα/2 = z0.05/2 = z0.025
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
0.5 - 0.025 = 0.4750
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.4750, y dicho valor es de z = 1.96.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:
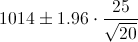
El intervalo de confianza bilateral al 95% es:
[1003.043267, 1024.956733]
Para obtener el tamaño que satisfaga un error de 5 horas al 95%, usamos la siguiente expresión matemática:
Como disponemos de todos los datos, sustituimos el parámetro que nos interesa y obtenemos la solución a este problema:
Por lo tanto, para satisfacer las condiciones del problema, el error debe ser menor de 5 horas, el tamaño de la muestra debe ser el número entero mayor al obtenido, por lo tanto, n = 97.
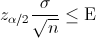
3 comentarios:
Hola, ¿de dónde se obtiene la expresión matemática del error?
Gracias por el blog!
Buenas:
El error para cada caso y distribución se obtiene matemáticamente, para no aprendernos todos los tipos existe una regla general y con las tablas por delante es bastante fácil.
Las colas o expresión de suma o diferencia es el error, por ejemplo, para un intervalo de confianza del parámetro media con varianza conocida, el intervalo de confianza es:
· X ± zα/2 · σ/√n
Pues el error sería:
· E ≤ zα/2 · σ/√n
Un saludo y gracias por tu comentario.
Hola me podrias ayudar con este. es parecido 2. Se sabe que la duración, en horas, de un foco de 75 watts tiene una distribución aproximadamente normal, con una desviaciónestándar de
σ = 29 horas. Se toma una muestra aleatoria de 32 focos, la cual resulta tener una duración promedio de x =1035 horas
¿Existe evidencia que apoye la afirmación de que la duración promedio del foco es mayor que 1000 horas? Utilice α = 0.01
Publicar un comentario