Ej6. La elasticidad de un polímero es afectada por la concentración de un reactivo. Cuando se utiliza una concentración baja, la elasticidad promedio verdadera es de 55, mientras que cuando se emplea una concentración alta, la elasticidad promedio es de 60. La desviación estándar de la elasticidad es 4, sin importar cuál sea la concentración.
Si se toman dos muestras aleatorias de tamaño 16, calcula la probabilidad de que 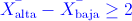 .
.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· Elasticidad Baja: μ2 = 55, σ2 = 4.
· Elasticidad Alta: μ1 = 60, σ1 = 4.
Para ambas concentraciones de elasticidad, el tamaño de la muestra es de 16.
Por lo tanto, aplicamos la Teoría Central del Límite para Dos Variables, en cada apartado:
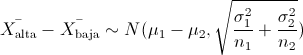
Las variables normalizadas queda:
Nos piden la siguiente probabilidad:
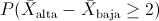
Tipificamos a la normal:
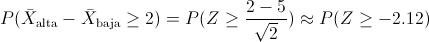
Operamos la desigualdad:
Buscamos en la tabla de la normal y sustituimos valores para obtener la solución a este problema:

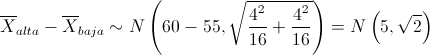




4 comentarios:
En el problema 6 del tema 5 ,¿no debería ser "n2" 16 en vez de 9?.Gracias por el blog y gracias de antemano. Slaudos.
Buenas:
Tienes razón, es más, si te das cuenta, los resultados obtenidos están bien, simplemente ha sido un fallo al escribir la expresión en LaTeX.
Ya ha sido subsanado el error, muchas gracias por advertirlo.
Un saludo.
Primero,gracias por todo,porque ayuda muchisimo el blog,en el principio en la formula de teoria central del limite pone que es(u1 - u2) pero pone (60 - 55),no deberia ser al reves?gracias.
Buenas:
Realmente es un error de nomenclatura, si te das cuenta, en el enunciado del problema nos piden calcular la probabilidad siguiente:
· X_ALTA - X_BAJA >= 2
Por lo tanto, se supone lo siguiente:
· Elasticidad Baja: μ_2.
· Elasticidad Alta: μ_1.
Yo los he nombrado al revés debido al orden de aparición en el enunciado del problema.
Aún así, ya está corregido y solucionado para que no haya malas interpretaciones.
Muchas gracias por la corrección y por tú comentario.
Un saludo.
Publicar un comentario