Ej5. Se toma una muestra aleatoria de tamaño n1 = 16 de una población normal que tiene una media de 75 y una desviación estándar de 8. De otra población normal, se toma una muestra aleatoria de tamaño n2 = 9. Esta última población tiene una media de 70 y una desviación estándar de 12.
Sean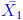 
y 
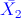las medias muestrales de cada muestra aleatoria respectivamente. Calcular la probabilidad de que:
a)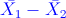 
sea mayor que 4.
b) 
.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· Muestra 1: n1 = 16, μ1 = 75, σ1 = 8.
· Muestra 2: n2 = 9, μ2 = 70, σ2 = 12.
Por lo tanto, aplicamos la Teoría Central del Límite para Dos Variables, en cada apartado:
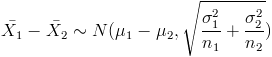
Las variables normalizadas queda:
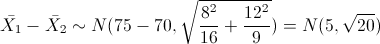
Apartado a)
Nos piden la siguiente probabilidad: P(X1 - X2 > 4).
Operamos la desigualdad: P(X1 - X2 > 4) = 1 - P(X1 - X2 ≤ 4)
Tipificamos:
1 - P(Z ≤ -0.22) = 1 - P(Z ≥ 0.22) = 1 - [1 - P(Z < 0.22)] = 0.5 + Φ(0.22)
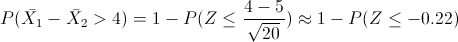
Buscamos en las tablas de la normal y sustituimos valores para obtener la solución a este apartado:
P(X1 - X2 > 4) = 0.5 + Φ(0.22) = 0.5 + 0.0871 = 0.5871
Apartado b)
Nos piden la siguiente probabilidad: P(3.5 ≤ X1 - X2 ≤ 5.5):
Tipificamos:
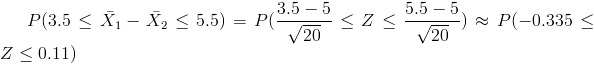
Por lo tanto, obtenemos:
P(-0.335 ≤ Z ≤ 0.11) = (0.5 + Φ(0.11)) - [1 - (0.5 + Φ(0.335))] = Φ(0.11) + Φ(0.335)
Buscamos en las tablas de la normal, pero no encontramos el valor exacto para 0.335, por lo que interpolamos linealmente:
..0.33...........0.335.......0.34
0.1293............P.........0.1331
De donde:
0.33 - 0.34.-> 0.1293 - 0.1331
0.33 - 0.335.-> 0.1293 - P
Calculamos:
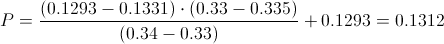
Sustituimos valores y obtenemos la solución a este apartado:
P(-0.335 ≤ Z ≤ 0.11) = Φ(0.11) + Φ(0.335) = 0.0438 + 0.1312 = 0.175
4 comentarios:
Buenas,gracias por el blog! en el primer apartado a) pone al principio,operamos la desigualdad...porque?no se puede usar ya directamente asi (X1 - X2 > 4) .un saludo y gracias!
Buenas:
Mientras hagas las cosas correctamente, puedes representar todo los datos como quieras.
En nuestro caso, se manipula la expresión ya que nuestras tablas, las cuales puedes descargarte gratuitamente desde el blog, tienen un formato especial, es decir, en el caso de la Distribución Normal, centra la campana de Gauss (la curva que describe la Distribución Normal) y solo opera con los valores positivos (ya que la curva es simétrica).
Es por ello, que adaptamos los datos a las necesidades de nuestras herramientas (en este caso, a las necesidades de nuestra tabla de la Distribución Normal), para que no haya confusión alguna y obtengamos el resultado correcto.
· PD: Nuestras tablas, son iguales a las que, prácticamente te vas a encontrar en cualquier libro de estadística.
Un saludo y muchas gracias por tú comentario.
la P(X1-X2 > 4) no deberia ser 0.5 -0,0871 ? ya que 1-(0,5+0,0871) = 1-P(x1-x2 < 4)
Buenas:
¡Cuidado! La expresión ya está desarrollada en el Apartado a), fíjate como:
· P(X1 - X2 > 4) = 1 - P(X1 - X2 ≤ 4) = {TIPIFICAMOS} = 1 - P(Z ≤ (4 - 5)/√20) ≈ 1 - P(Z ≤ -0.22)
Después desarrollas el resultado como está expuesto en el Apartado a) y la solución es correcta.
Un saludo.
Publicar un comentario