Ej4.El tiempo que un pasajero invierte esperando en un punto de revisión de un aeropuerto es una variable aleatoria con media de 8.2 minutos y desviación estándar de 1.5 minutos. Supongamos que se observa una muestra aleatoria de 49 pasajeros.
Calcula la probabilidad de que el tiempo de espera promedio para estos clientes sea:
a) Menor que 10 minutos.
b) Entre 5 y 10 minutos.
c) Menor que 6 minutos.
Sea la variable aleatoria X, tiempo promedio en un punto de revisión de un aeropuerto. Conocemos tanto la media, 8.2 minutos, como la desviación estándar, 1.5 minutos y el tamaño de la muestra, que es de 49 pasajeros.
Por lo tanto, aplicamos la Teoría Central del Límite para cada apartado:
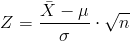
Apartado a)
Nos piden la siguiente probabilidad: P(X < .10):
Tipificamos:
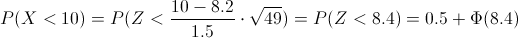
En las tabas, a partir del 3.99, la probabilidad obtenida es de 0.5, por lo tanto, la solución a este apartado es:
Apartado b)
Nos piden la siguiente probabilidad: P(5 ≤ X ≤.10):
Tipificamos:
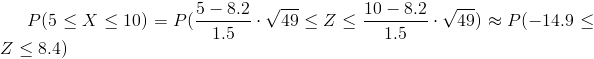
Por lo tanto, obtenemos:
Buscamos en las tablas, y nos ocurre lo mismo que en el Apartado a), a partir del valor 3.99, la probabilidad es 0.5, por lo tanto:
Apartado c)
Nos piden la siguiente probabilidad: P(X < .6):
Tipificamos:
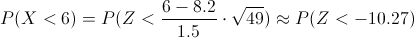
Operamos la desigualdad: P(Z < .-10.27) = P(Z > 10.27) = 1 - P(Z ≤ 10.27)
Buscamos en las tablas, y nos ocurre lo mismo que en el Apartado a), a partir del valor 3.99, la probabilidad es 0.5, por lo tanto:





1 comentarios:
en el apartado b, cuando calculas el area de una region de la campana de gauss, y z es negativo: 0.5-P(Z<Zo), por lo tanto el resultado del apartado b seria 0, no 1. gracias
Publicar un comentario