Problema12: VAC

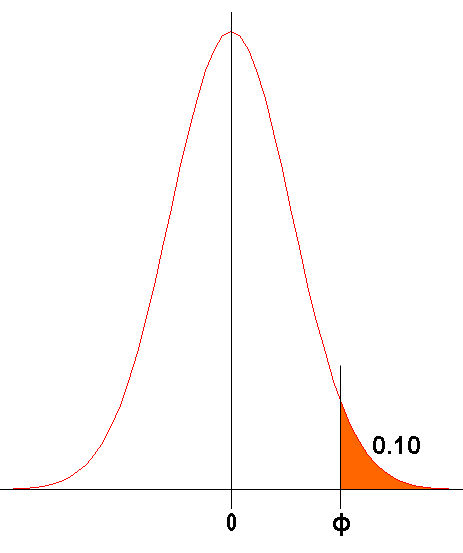
Ej12. Suponga que la maestra de un enorme grupo dice que es necesario obtener una nota ubicada en el 10% superior de la distribución de calificaciones de la clase para sacar una A en un examen particular.

Por experiencia, ella puede estimar que la media y la desviación estándar de este examen serán de 72 y 13 respectivamente. Teniendo en cuenta que las calificaciones tienen una distribución normal, ¿cuál es la calificación mínima necesaria para obtener una A?

Sea la variable aleatoria X, la calificación mínima para obtener una A.

Los datos que nos ofrecen son los siguientes:

P(X ≥ x) = 0.10

Es decir, debemos obtener la calificación mínima para obtener una nota de A sabiendo que, la probabilidad es 0.10 y que la media es de 72 y su desviación estándar es de 13.

Nos hacemos una idea gráfica de lo que tenemos:

Observamos, que este es un típico problema de una resolución inversa, nos dan los datos de la probabilidad y nos piden el valor de la variable aleatoria para dicha probabilidad.

Adecuamos los datos a las tablas que dispone Aqueronte:

0.50 - 0.10 = 0.40

Por lo tanto, buscamos en la tabla el valor de 0.40 para obtener el Φ(x), y en este caso, no se dispone del valor exacto, por lo tanto, interpolamos linealmente:

..1.28.................Z................1.29
0.3997............0.4.............0.4015

De donde:

0.3997 - 0.4015....-> 1.28 - 1.29
0.3997 - 0.4..-> 1.28 - Z

Calculamos:

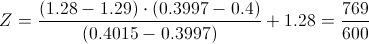
Por lo tanto, ahora disponemos de los datos necesarios para obtener la calificación mínima necesaria para obtener una A con una probabilidad del 10%:

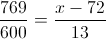
Despejamos la variable y obtenemos: x = 53197/600.

Aproximadamente, la calificación mínima para obtener una calificación de A con una probabilidad de un 10% es de: x = 89.