Problema11: VAC

Ej11. Considere los valores del coeficiente intelectual (C.I.) de las personas. Estos valores están distribuidos normalmente con una media de 100 y una desviación estándar de 16. Si se elige una persona al azar, obtener:

a) La probabilidad de que su coeficiente intelectual esté entre 100 y 115.

b) La probabilidad de que su coeficiente intelectual sea mayor que 90.


Apartado a)

Sea la variable aleatoria X, el coeficiente intelectual de una persona elegida al azar.

Nos piden obtener la siguiente probabilidad:

P(100 < X < 115)

Pero nos indican que X sigue una distribución normal, por lo tanto, debemos tipificar los datos dados:

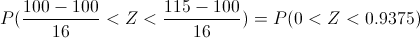
Por lo tanto:

P(0 < Z < 0.9375) = Φ(0.9375) - Φ(0)

Buscamos en las tablas de la Normal dichos valores, pero nos encontramos con un problema, y es que las tablas disponibles en Aqueronte sólo disponen de dos decimales, así qué tenemos dos opciones, redondear o aproximar mediante interpolación lineal o realizando la media. Vamos a realizar los tres casos.

Redondeando:

P(0 < Z < 0.94) = Φ(0.94) - Φ(0) = 0.3264 - 0 = 0.3264

Interpolación Lineal:

..0.93.................0.9375................0.94
0.3238...................P....................0.3264

De donde:

0.93 - 0.94....-> 0.3238 - 0.3264
0.93-0.9375..-> 0.3238 - P

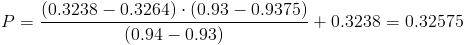
Por lo tanto:

P(0 < Z < 0.9375) = Φ(0.9375) - Φ(0) = 0.32575 - 0 = 0.32575

Realizando la media:

..0.93.................................0.94
0.3238.............................0.3264

De donde:

Z = (0.93 + 0.94)/2 = 0.935
P = (0.3264 + 0.3238)/2 = 0.3251

Por lo tanto:

P(0 < Z < 0.935) = Φ(0.935) - Φ(0) = 0.3251 - 0 = 0.3251

Apartado b)

En este caso, nos piden obtener la siguiente probabilidad: P(X > 90).

Como X sigue una distribución normal, tipificamos los datos:

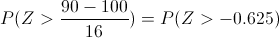
Operamos la desigualdad:

P(Z ≤ 0.625) = 0.5 + Φ(0.625)

Como las tablas que dispone Aqueronte sólo contiene dos cifras decimales, obtenemos el valor requerido mediante interpolación lineal.

Interpolación Lineal:

..0.62.................0.625................0.63
0.2324...................P.................0.2357

De donde:

0.62 - 0.63....-> 0.2324 - 0.2357
0.62-0.625..-> 0.2324 - P

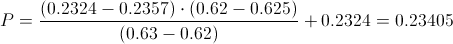
Por lo tanto, la solución a este apartado es:

P(Z ≤ 0.625) = 0.5 + Φ(0.625) = 0.5 + 0.23405 = 0.73405