Ej13. El administrador de un lote de automóviles, prueba dos marcas de llantas radiales. Para ello, asigna, al azar, una llanta de cada marca a las dos ruedas posteriores de ocho automóviles, y luego corre los automóviles hasta que las llantas se desgastan. Los datos obtenidos, en kilómetros, son los siguientes:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| marca 1 | 36925. | 45300. | 36240. | 32100. | 37210. | 48360. | 38200. | 33500 |
| marca 2 | 34318 | 42280 | 35500 | 31950 | 38015 | 47800 | 37810 | 33215 |
Encuentre un intervalo de confianza del 99%, para la diferencia del número de kilómetros medio de duración. Con base a estos cálculos, ¿qué llanta dura más?
Este problema lo podemos resolver de dos formas, la primera: Considerándose las muestras pareadas, y la segunda: Como muestras independientes.
Lo resolveremos de ambas formas y veremos las diferencias de ambos métodos.
Solución mediante Muestras Pareadas.
Para ello, debemos restar los datos de las muestras dadas una a una, obteniéndose la siguiente tabla:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Diferencia | 2607 | 3020 | 740 | 150 | .-805 | .560 | 390 | 285 |
Calculamos los datos estadísticos básicos.
Para obtener la media:
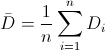
Por lo tanto:
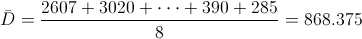
Para obtener la cuasi varianza:
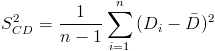
Por lo tanto, la cuasi desviación estándar:
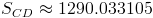
En este problema nos pide realizar un intervalo de confianza para la diferencia de medias con varianza desconocida y tamaño de la muestra es menor que 30:
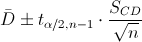
Para una confianza del 99%, obtenemos α:
100(1 - α) = 99
Despejamos el parámetro que nos interesa: α = 0.01. El siguiente paso es obtener los valores de:
· tα/2,n-1 = t0.01/2,8-1=t0.005,7
Buscamos el valor en la tabla t-Student, y obtenemos: 3.4995.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la diferencia de medias con un 99%, simplemente, sustituimos valores:
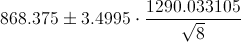
El intervalo de confianza bilateral al 99% es:
[-727.731476, 2464.481475]
Al contener en cero en el intervalo de confianza, no existen evidencias de que significativas para decir que una llanta dure más que otra.
Solución mediante Diferencias de Medias.
Nos encontramos con un problema, las varianzas son desconocidas de ambas muestras pero no sabemos si son iguales o no y con medias desconocidas igualmente. Esto es importante ya que dependiendo de dicho matiz, cambia la forma de resolver el problema.
Por lo tanto, lo primero que debemos hacer, es una prueba de hipótesis para dictaminar si ambas varianzas desconocidas son iguales o no.
Tomo como hipótesis nula que ambas varianzas son iguales, siendo la hipótesis alternativa, que no lo son:
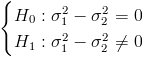
Cuyo estadístico es:
Pero antes, debemos obtener la cuasi desviación típica de cada muestra:
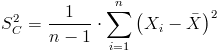
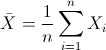
Por lo tanto:
· 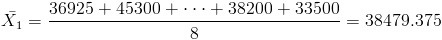
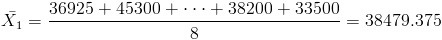
·
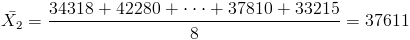
Por lo tanto, para cada marca de neumáticos:
· SC1 ≈ 5590.278831
· SC2 ≈ 5243.908112
Ya disponemos de los datos necesarios para obtener el valor del estadístico:
Para ver si aceptamos la hipótesis nula, debemos calcular la región crítica y evaluar los resultados obtenidos. La región crítica para este estudio es:
F ≥ Fα/2,n1 - 1, n2 - 1 , F ≤ F1-α/2, n1 - 1, n2 - 1
Para una confianza del 99%, obtenemos α:
100(1 - α) = 99
Despejamos el parámetro que nos interesa: α = 0.01. Por lo tanto:
F ≥ F0.005, 7, 7 , F ≤ F0.995, 7, 7
Hay que tener en cuenta que:
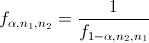
Buscamos en la tabla de F de Snedecor:
· F0.005, 7, 7 = 8.89
· F0.995, 7, 7 = 1/F0.005, 7, 7 = 1/8.89 = 100/889 ≈ 0.112486
Para aceptar la hipótesis nula, el estadístico calculado (1.136467) debe estar dentro del intervalo:
(0.112486, 8.89)
Y nuestro estadístico, está dentro de dicho intervalo, por lo que aceptamos la Hipótesis nula de que ambas varianzas son iguales.
Una vez que sabemos que la varianza de ambas muestras son iguales, pasamos a confeccionar el intervalo de confianza para la diferencia de medias.
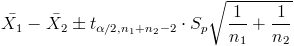
Para una confianza del 99%, obtenemos α:
100(1 - α) = 99
Despejamos el parámetro que nos interesa: α = 0.01. El siguiente paso es obtener los valores de:
· tα/2,n1+n2-2 = t0.01/2,8+8-2 = t0.005, 14
Buscamos el valor en la tabla t-Student, y obtenemos: 2.9768.
Necesitamos obtener el valor de Sp:
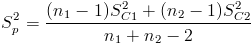
Tenemos todos los datos necesarios para obtener su valor, por lo tanto sustituimos valores:
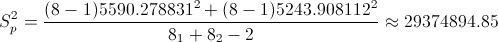
Ya disponemos todos los datos necesarios para obtener el intervalo bilateral de confianza al 99% de la diferencia de medias con varianzas desconocidas e iguales:
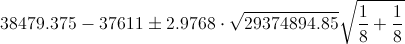
El intervalo de confianza bilateral al 99% es:
[-7198.546331, 8935.296331]
Al contener el cero en el intervalo de confianza, no existen evidencias significativas para decir que una llanta dure más que otra.
Como hemos podido observar, ambas formas de resolver el problema dado dan el mismo resultado, eso sí, el segundo método es mucho más meticuloso en su procedimiento que el primero, considerando pruebas pareadas.

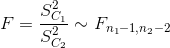
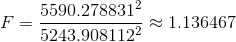




15 comentarios:
en la solucion mediante muestras pareadas, la Sc no deberia ser con raiz cuadrada al hallar al final el intervalo??
ah no perdon, que ya estaba hecha la raiz anteriormente
Muchísimas gracias por tu publicación
buscaba un ejemplo parecido, muchas gracias!!!
Buenas Ikary:
Me alegro que te haya servido de ayuda.
Gracias por tu comentario y un saludo.
hola muy buenas, ante todo felicitarle por su blog, es muy completo y claro.
solo comentarte que me surge una duda cuando resuelves el problema de la segunda forma (Solución mediante Diferencias de Medias), a mi entender, en el enunciado no nos proporcionan la media, por lo que yo usaria contrastes sobre igualdad de varianzas con medias desconocidas(donde necesitamos Sc^2 que se calcula mediante la media muestral que es fácil de hallar con los datos que nos proporciona el enunciado.). En cambio tu usaste contrastes sobre igualdad de varianzas con medias conocidas, y no se de donde sacaste la media(calculaste la media muestral)
Buenas:
Tienes razón, se debería hallar con el contraste sobre: Igualdad de varianzas con medias desconocidas.
En dos o tres semanas máximo, lo tendré arreglado.
Gracias por el apunte, un saludo.
Hola buenas
Queria recordarle el error que tiene el ejercicio en la segunda parte, que seguramente se le ha olvidado arreglarlo como decia en su comentario
Saludos, Miguel
Buenas:
Ya está subsanado y actualizado el problema con la correcta resolución.
Gracias por el apunte, un saludo.
Hola que tal
Tengo una duda con la segunda parte del ejercicio. Para resolver el ejercicio ha utilizado la formula de las poblaciones normales a pesar de que el enunciado no dice de manera explicita que se trate de una distribucion normal. Por eso, cuando estaba resolviendo el ejercicio yo lo hice utilazando la formula de las poblaciones generales para n>30 que no te exigen conocer la igualdad la varianza.
Entonces, la pregunta es como se debe actuar en estos casos? De la forma en la que lo he hecho estaria mal?
Muchas gracias, un saludo
Miguel Angel
Buenas Miguel Ángel:
Tú mismo te respondes a escribirlo pero sin darte cuenta, vamos a ver, la expresión que has usado es la siguiente (según tú comentario):
· Poblaciones generales para n > 30.
Mi pregunta es, ¿en este ejercicio tenemos una muestra n1, n2 > 30?
La respuesta es NO (nuestra muestra es n1, n2 = 8). Por lo tanto, la expresión que has usado no corresponde con las especificaciones del enunciado de este problema.
Respecto a si el enunciado dice o no que estamos antes una distribución Normal, he de decir, que se presupone, ya que estos ejercicios están dentro del capítulo: Estimación Y Pruebas de Hipótesis Paramétricos.
· PD: A ver si saco un poco de tiempo y añado al curso de Estadística el capítulo de Estudios No Paramétricos (donde deberemos resolver si un conjunto de datos sigue una distribución en concreto o la podemos aproximar).
Un saludo.
¿Faltaría parte del enunciado?
Muchas gracias por el blog.
Buenas:
El enunciado está completo, ¿a qué te refieres con que falta parte del enunciado?
Un saludo.
Respecto a el fallo del enunciado, error mio. Cosa del explorador. Lo siento, también he comentado del 12 al 14 creo.
Muchas gracias
Esto esta mal, se hace mediante pruebas no parametricas puesto que no se menciona que la distribucion sea normal. Por lo tanto al ser muestras pareadas se hace con Prueba de signos. Ambas soluciones estan mal, puesto que se debe resolver con los datos que se tiene y no asumir distribucion normal, sino se puede demostrar con prueba de ajuste. Por lo tanto yo te jalaria si me colocas esas dos soluciones.
Disculpa de dónde sacaste el 1290?
Publicar un comentario