Ej13. Los ingresos de los ejecutivos junior en una gran empresa están distribuidos normalmente con una desviación estándar de 1200$. Se piensa hacer un recorte de personal, por lo que los empleados que ganan menos de 28000$ serán despedidos.
Si el despido representa al 10% de tales ejecutivos, ¿cuál es el salario medio actual del grupo de ejecutivos junior?
Sea la variable aleatoria X, el salario de los ejecutivos junior.
Los datos que nos ofrecen son los siguientes:
P(X ≤ 28000) = 0.10
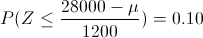
Adaptamos los datos dados a las tablas disponibles en Aqueronte:
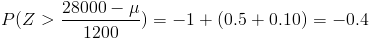
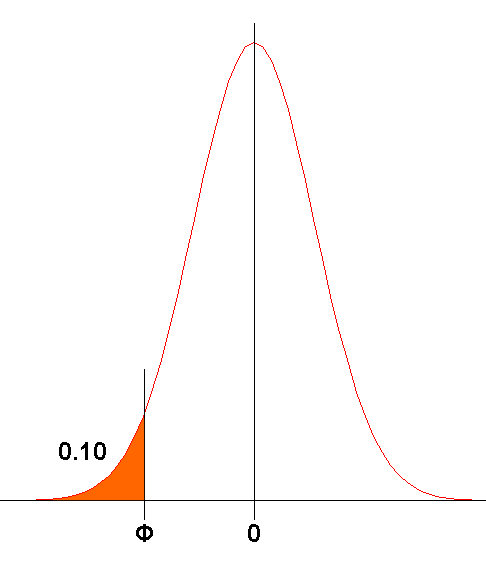
Es negativo ya que la probabilidad se encuentra en el semieje negativo X, gráficamente se ve más claro:
Buscamos en la tabla el valor de -0.40, y en este caso, no se dispone del valor exacto, por lo tanto, interpolamos linealmente:
..-1.28................-Z................-1.29
-0.3997............-0.4.............-0.4015
De donde:
-0.3997 + 0.4015....-> -1.28 + 1.29
-0.3997 + 0.4..-> -1.28 + Z
Calculamos:
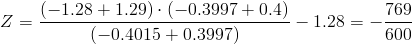
Por lo tanto, ahora disponemos de los datos necesarios para obtener el salario medio actual de los ejecutivos junior:
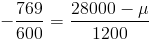
Despejamos el valor medio y obtenemos la solución al problema: μ = 29 538$.





4 comentarios:
creo que hay un error cuando dice que
P(Z> 28000-u/1200) = -1 +(0.5 0'10)= -0.4
primero a mi no me cuadra eso del -1, ni tampoco lo de 0'5 mas 0'10, no se de donde lo sacas, pero lo que yo creo que esta mal de verdad es el -0'4, una probabilidad no puede ser negativa nunca.
me corrijo. no he dicho nada sobre lo de 0'5 mas 0'1. pero lo del -1 y -0'4 sigo pensando q esta mal
Buenas:
Tanto el resultado como el modo de operación están bien.
Es cierto que ninguna probabilidad puede ser negativa ni mayor a 1, pero ojo, esto es así por la consideración previa de escala que se ha tomado.
En otras palabras, yo puedo medir la probabilidad multiplicando por 100 o multiplicando por -100, ésto no me cambiaría el resultado final pero sí la escala con la cuál lo estaría evaluando.
En el estudio de la Normal, su curva es relativamente peculiar, ya que es simétrica, es por ello que para trabajar mediante tablas es más cómodo situar el origen de coordenadas en el centro de la campana de Gauss (curva de la Normal) y quedarnos, en este caso, con el semieje positivo.
Ahora bien, tenemos que tener en cuenta que con este cambio de escala (μ = 0), sólo tenemos los datos del semieje positivo relativos al origen: P(Z ≤ x), y es por ello, que debemos sumar 0.5 al valor encontrado en tablas por compensación de la mitad restante de la curva de la Normal.
Bueno hasta aquí sencillo, pero ¿y si el valor estadístico en vez de estar en la cola de la derecha, está en la izquierda?
Pues es lo que pasa en este ejemplo, forzosamente, por la escala que tenemos planteada en nuestra tabla de la Normal, dará un valor negativo porqué dicho valor estará a la izquierda del punto central, y por ende, todo número menor de cero es negativo.
Y cosa importante, en las tablas no tenemos referencia del valor en la parte izquierda de la curva, pero es indiferente este dato ya que al ser simétrica, empleamos el valor de la parte derecha y le asignamos el signo negativo.
Hasta aquí, creo que ya he explicado el por qué del valor negativo, no es más que por la escala que hemos tomado, es decir, el origen está en el centro justo de la curva de la Normal.
Lo siguiente que no te cuadra es lo del -1.
Como he dicho anteriormente, los datos que tenemos en las tablas están referenciados al origen, si ves la gráfica esquemática del problema, comprobarás que la probabilidad que tenemos que hallar es justamente la de la cola izquierda la cual, no está referenciada al origen, es por ello que debemos restarle 1, para obtener el valor respecto al origen que es el que tenemos tipificado en tablas.
Bueno, espero que me haya explicado bien, pero realmente, en este ejercicio he intentado realizarlo exhaustivamente, es decir, siguiendo todos los pasos.
Podemos evitar algunos aplicando la propia definición de la tipificación a la Normal:
· P(Z ≤ x) = 0.5 + Φ(z) = 0.1
Despejamos: Φ(z) = 0.1-0.5 = -0.4.
En otras palabras, los valores que el enunciado nos ofrece de probabilidad están referenciados a toda la curva de la Normal, pero nosotros, al tener las tablas adaptadas, el origen en el centro de la curva, debemos restar siempre 0.5 que corresponde a la parte de la curva que no tenemos tipificada en tablas.
Y como bien he dicho, también, anteriormente, el no tener tipificada la otra parte de la curva es irrelevante para la solución del problema, ya que al ser simétrica la campana de Gauss, ambos datos serán idénticos pero con signo contrario.
Espero haberte solucionado el problema que tenías, gracias por tu comentario.
si, muchas gracias por aclararmelo. me ha sido de gran ayuda. excelente blog. felicidades por el
Publicar un comentario