Ej14. Para un grupo de hombres adultos con una edad particular, la distribución de lecturas de colesterol, en mg/dl, se distribuye normalmente con una media de 210 y una desviación estándar de 15.
Obtener:
a) La probabilidad de esta población que tengan lecturas que excedan los 250.
b) La probabilidad de esta población que tengan lecturas inferiores a 180.
Sea la variable aleatoria X, lecturas de colesterol en mg/dl. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Apartado a)
Nos piden obtener la siguiente probabilidad: P(X > 250)
Tipificar los datos dados:
Operando la desigualdad:
P(Z > 2.67) = 1 - P(Z ≤ 2.67) = 1 - [0.5 + Φ(2.67)]
Buscamos en las tablas de la Normal dichos valores y resolvemos este apartado:
P(Z > 2.67) = 1 - [0.5 + 0.4962] = 0.0038
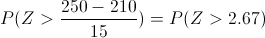
Apartado b)
En este caso, nos piden obtener la siguiente probabilidad: P(X < 180), sabiendo que X sigue una distribución normal, tipificamos los datos:
Operamos la desigualdad:
P(Z < -2) = P(Z > 2) = 1 - P(Z ≤ 2) = 1 - [0.5 + Φ(2)]
Obtenemos el valor de las tablas de la normal y resolvemos este apartado:
P(Z < -2) = 0.5 - Φ(2) = 0.5 - 0.4772 = 0.0228
5 comentarios:
Hola,me gustaría saber por qué a 0,5 hay que sumarle o restarle el valor que hemos tomado de la tabla.
Gracias.
Buenas:
Al ser la curva de la Normal (la campana de Gauss) simétrica, para facilitar los datos, ponemos los ejes X e Y justo en el centro de la curva.
Por este motivo, sólo estamos usando la mitad de valores de la tabla, es por ello que debemos sumar la otra mitad para obtener el valor de área completa.
Teniendo en cuenta que asumimos que la máxima probabilidad es de 1 (no existe probabilidad, sólo una evidencia), debemos sumar 0.5 que corresponde a la parte que nos dejamos fuera por considerar los ejes en la posición central de la curva.
Un saludo.
Al final del apartado B, en vez de:
P(Z > -2) = 0.5 - Φ(2) = 0.5 - 0.4772 = 0.0228
¿No sería lo siguiente?
P(Z > -2) = 0.5 + Φ(2) = 0.5 + 0.4772 = 0.0228
Ya que estamos buscando valores de Z por encima del valor del área de cola de Z=-2. Como es un número negativo, estaría en la parte izquierda de la tabla, y todos los valores de Z mayores a ese, serían los situados del eje Y hasta Z=-2, es decir 0.4772, y todos los de la parte derecha, 0.5.
Muchas gracias por el blog.
Buenas:
En el Apartado b) había una errata, donde ponía:
· P(Z > -2)
Quería decir:
· P(Z < -2)
Tal y como el procedimiento del problema lo iba indicando.
Un saludo y perdón por la confusión.
Muchas gracias
Publicar un comentario