Problema2: Estimación y Pruebas de Hipótesis

Ej2. Sean 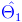, y tres estimadores del parámetro θ, se sabe que:
·

·

·

·

·

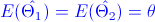
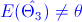
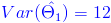
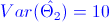
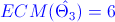
Realizar una comparación de los tres estimadores. ¿Cuál sería el mejor estimador de θ?.


Calculamos el sesgo para cada estimador:

· Sesgo del Estimador 1: sesgo1 = θ - θ = 0
· Sesgo del Estimador 2: sesgo2 = θ - θ = 0
· Sesgo del Estimador 3: Nos dan el error cuadrático medio.

Para ver, que estimador es mejor, hallamos el error cuadrático medio de cada estimador:

.

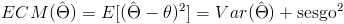· ECM 1 = 12
· ECM 2 = 10

· ECM 3 = 6

Para saber cual estimador es mejor, usamos el cociente del error cuadrático medio:

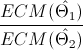
Entre el estimador 1 y el estimador 2:

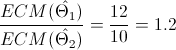
El resultado es mayor que 1, por lo que el estimador 2 es más eficiente que el estimador 1. Hallaremos cual es mejor entre el estimador 2 y el estimador 3:

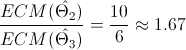
El resultado es mayor que 1, por lo que el estimador 3 es más eficiente que el estimador 2.

Por lo tanto, el estimador más eficiente para el parámetro θ es el estimador 3.