Ej1. Sean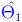 
y 
dos estimadores del parámetro θ, tales que:
· 
· 
· 
· 
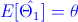
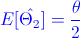
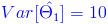
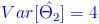
¿Qué estimador es mejor?.
Calculamos el sesgo para cada estimador:
· Sesgo del Estimador 1: sesgo1 = θ - θ = 0
· Sesgo del Estimador 2: sesgo2 = θ - θ/2 = θ/2
Podemos observar, que el estimador 1 es insesgado, mientras que el estimador 2, es sesgado.
Para ver, que estimador es mejor, hallamos el error cuadrático medio de cada estimador:
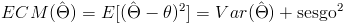.· ECM 1 = 10
· ECM 2 = 4 + (θ/2)2
· ECM 2 = 4 + (θ/2)2
Para saber cual estimador es mejor, usamos el cociente del error cuadrático medio:
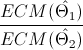
Sustituyendo valores:
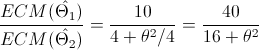
Para que el estimador 1 sea mejor que el estimador segundo, se debe corroborar:
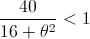
Despejamos:
40 < . 16 + θ2
Por lo tanto, para que el estimador 1 sea más eficiente que el estimador 2, se debe cumplir: θ2 > 24.
1 comentarios:
Hola, antes de nada agradecerle el tiempo que le dedica a este blog, muy bueno de verdad, tengo una duda con un ejercicio haber si me podia ayudar, el siguiente: para estimar el parámetro m= E(X) a partir de la m.a.s X1,..,Xn de la v.a. X, disponemos de los estimadores m^1 y m^2 = (5X1 - 2Xn)/3, la esperanza y la varianza de m^1 son m y 3o2 respectivamente, donde o2 = VAR(X), nos piden el ECM mas pequeño y la consistencia.
Gracias.
Saludos.
Publicar un comentario