Estimación y Pruebas de Hipótesis.

En este capítulo se abordará las expresiones matemáticas básicas para la Estimación y Pruebas de Hipótesis.

Normalmente, se suele denominar: Inferencia Estadística, que no es más que, los métodos utilizados para tomar decisiones o para sacar conclusiones sobre una población. Para ello, se utilizan la información contenida en una muestra de la población.


Estimación Puntual.

Sea θ, un parámetro desconocido de la población de interés, y sea X1, X2, ..., Xn una muestra aleatoria de tamaño n de dicha población. Se llama estimador puntual θ, al estadístico que se usa para estimar el valor del parámetro θ.

Por lo tanto, un estimador puntual del parámetro θ de una población, es un valor numérico del estimador puntual .

· Estimador Insesgado para el parámetro θ: .

· Sesgo del estimador : .

· Error Cuadrático Medio: .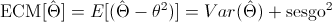

Sean y dos estimadores puntuales para el parámetro θ. Se define la eficiencia relativa de con respecto a como el cociente:

Si dicha cantidad es menor que 1, entonces decimos que es más eficiente que .

· Estimador de Máxima Verosimilitud de θ: Sea X una variable aleatoria con función de probabilidad (o densidad de probabilidad) f(x, θ), donde θ es un parámetro desconocido. Sean x1, x2, ..., xn los valores observados de una muestra aleatoria de tamaño n de X.

La función de verosimilitud de la muestra es:

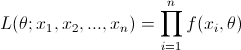
El estimador de máxima verosimilitud de θ, es el valor de θ que maximiza la función de verosimilitud.


Teoría Central del Límite.

Sea X1, X2, ..., Xn una muestra aleatoria de tamaño n de una distribución con media μ y varianza σ². Entonces, el límite de la distribución de:

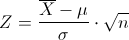
Cuando n -> ∞, es la distribución normal estándar.

Sean X1 y X2 dos poblaciones normales independientes con medias μ₁ y μ₂, y varianzas σ²₁ y σ²₂. Si y son las medias muestrales de dos muestras aleatorias independientes de tamaños n1 y n2 de estas poblaciones, entonces:

Teoría Central del Límite para Dos Variables.

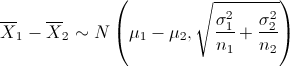
Si en las condiciones de la Teoría Central del Límite, las variables X1 y X2 no siguen distribuciones normales, entonces, el límite de la distribución es:

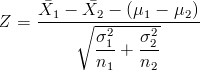
Cuando n1 y n2 -> ∞, es la distribución normal estándar.


Error Estándar.

El error estándar de un estadístico es la desviación típica de su distribución muestral. Si el error estándar involucra parámetros desconocidos de la población, cuyos valores pueden estimarse, entonces la sustitución de los parámetros por estas estimaciones en el error estándar, da como resultado el error estándar.

Por ejemplo: X ~ N(μ, σ), el error estándar de es .

Y el error estándar estimado de es .


Distribución Ji-Cuadrada.

Sean Z1, ..., Zk variable aleatorias normales independientes, con media μ = 0, y varianzas σ² = 1. Entonces, la variable aleatoria:

X = Z²₁ + ... + Z²_k

Tiene una función de densidad de probabilidad:

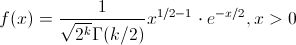
Y se dice que sigue una distribución ji-cuadrada con k grados de libertad. Se representa por X ~ X²_k.

· Esperanza: E(X) = k

· Varianza: V(X) = 2k.

· Puntos Críticos: X²α_{, k} es tal que: P(X > X²α_{, k}) = α.


Distribución t-Student.

Sean las variables aleatorias Z ~ N(0, 1) y V ~ X²_k. Si Z y V son independientes, entonces, la variable aleatoria es:

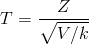
Tiene una función de densidad de probabilidad:

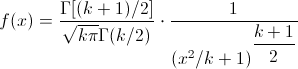
Para -∞ < . x < . ∞. Y se dice que sigue una distribución t-Student con k grados de libertad. Se representa por T ~ t_k.

Dicha función posee una curva simétrica y sus colas son más amplias que las de la distribución normal.

· Esperanza: E(X) = 0, para k > 2.

· Varianza: V(X) = k/(k-2), para k > 2.

· Puntos Críticos: tα_{, k} es tal que: P(T > tα_{, k}) = α.


Distribución F de Snedecor.

Sean X1 y X2 variables aleatorias ji-cuadradas independientes con grados de libertad k1 y k2 respectivamente. Entonces, la variable aleatoria es:

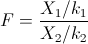
Tiene una función de densidad de probabilidad:

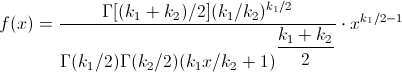
Para x > 0. Y se dice que sigue una distribución F de Snedecor con k1 grados de libertad en el numerador y k2 grados de libertad en el denominador. Se representa por F ~ F_k1,k2.

· Esperanza: , para k2 > 2.

· Varianza: , para k2 > 4.

· Puntos Críticos: fα_{, k1, k2} es tal que: P(F > fα_{, k1, k2}) = α.

Hay que tener en cuenta que: .


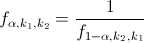Estimación Por Intervalos.

Una estimación por intervalos de un parámetro desconocido θ, es un intervalo de la forma [l, u], donde los extremos l y u, dependen de la estimación puntual para una muestra particular, y de la distribución muestral de .

Los extremos l y u son valores de las variables aleatorias L y U respectivamente y reciben el nombre de límites de confianza inferior y superior.

Pruebas de Hipótesis.

Una prueba de hipótesis estadística es un procedimiento que conduce a una decisión sobre una hipótesis. Esta decisión se toma a partir de una muestra aleatoria de la población de interés.

Si la información contenida en la muestra es consistente con la hipótesis, se concluye que ésta es verdadera. En otro caso, se concluye que ésta es falsa.

· H0 es la hipótesis que se desea probar.

· El rechazo de H0 conduce a la aceptación de H1.

· H0 se plantea siempre de modo que especifique un valor exacto del parámetro.

· La prueba de hipótesis involucra la toma de una muestra aleatoria, el cálculo de un estadístico a partir de la muestra aleatoria, y el uso del mismo para tomar una decisión sobre H0.

· Error Tipo I: Rechazo de H0 cuando H0 es verdadera.

· Error Tipo II: Aceptación de H0 cuando H0 es falsa.

· Nivel de significación α: Probabilidad de error del Tipo I.

· Nivel de significación β: Probabilidad de error del Tipo II.

Decisión	H0 es Verdadera	H0 es Falsa
Aceptar Ho	No hay Error	Error del Tipo II
Rechazar Ho	Error del tipo I	No hay Error

Los errores Tipo I y Tipo II están relacionados, una disminución en la probabilidad de uno, produce un aumento de la probabilidad del otro, siempre que el tamaño de la muestra no cambie, en general, un aumento de n reduce tanto a α como a β.

· p-Valor: Es el nivel de significación más pequeño que conduce al rechazo de H0.

Las distintas pruebas de hipótesis, se resumen en el fichero en formato .pdf, que se muestra a continuación:

Estimación y Pruebas de Hipótesis

---

Se puede descargar el formulario de este tema: Estimación, Intervalos de Confianza y Pruebas de Hipótesis, anteriormente mostrado, en el siguiente enlace:

		Estimación, Intervalos de Confianza y Pruebas de Hipótesis
		Estimación, Intervalos de Confianza y Pruebas de Hipótesis

---

A continuación, se disponen de una colección de problemas resueltos.

Problemas: Estimación, I.C. y Pruebas de Hipótesis.
Problema 1	Problema 11	Problema 21	Problema 31	Problema 41	Problema 51	Problema 61	Problema 71	Problema 81
Problema 2	Problema 12	Problema 22	Problema 32	Problema 42	Problema 52	Problema 62	Problema 72	Problema 82
Problema 3	Problema 13	Problema 23	Problema 33	Problema 43	Problema 53	Problema 63	Problema 73	Problema 83
Problema 4	Problema 14	Problema 24	Problema 34	Problema 44	Problema 54	Problema 64	Problema 74	Problema 84
Problema 5	Problema 15	Problema 25	Problema 35	Problema 45	Problema 55	Problema 65	Problema 75
Problema 6	Problema 16	Problema 26	Problema 36	Problema 46	Problema 56	Problema 66	Problema 76
Problema 7	Problema 17	Problema 27	Problema 37	Problema 47	Problema 57	Problema 67	Problema 77
Problema 8	Problema 18	Problema 28	Problema 38	Problema 48	Problema 58	Problema 68	Problema 78
Problema 9	Problema 19	Problema 29	Problema 39	Problema 49	Problema 59	Problema 69	Problema 79
Problema 10	Problema 20	Problema 30	Problema 40	Problema 50	Problema 60	Problema 70	Problema 80

Como caso particular, pongo aparte una colección de problemas para obtener el estimador de máxima verosimilitud de una función:

Problemas: Estimador de Máxima Verosimilitud.
Problema 1	Problema 6
Problema 2	Problema 7
Problema 3	Problema 8
Problema 4	Problema 9
Problema 5	Problema 10