Problema30: Estimación y Pruebas de Hipótesis

Ej30. Dos compañías de compuestos químicos pueden surtir materia prima. La concentración de un elemento en particular es este material es importante. La media de concentración de ambos proveedores es la misma, pero se sospecha que la variabilidad de la concentración puede diferir entre las dos compañías.

La cuasidesviación estándar de la concentración en una muestra aleatoria de n₁ = 15 lotes producidos por la compañía 1 es S_c1 = 4.7 g/l, mientras que para la compañía 2, una muestra de n₂ = 20 lotes proporciona un valor de S_c2 = 5.8 g/l

¿Existe evidencia suficiente para concluir que las varianzas de las dos poblaciones son diferentes?. Utiliza α = 0.05.


Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Compañía 1: n₁ = 15, S_c1 = 4.7.
· Compañía 2: n₂ = 20, S_c2 = 5.8.
· Nivel de significación: α = 0.05.
· Ambas medias, de las dos compañías, son iguales.

Calculamos lo que nos pide el problema: Contraste sobre igualdad de varianzas con medias desconocidas:

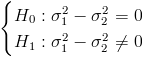
El estadístico es:

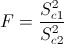
Obtenemos el valor del estadístico:

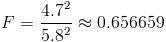
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

F ≤ f_{1-α/2,n1-1,n2-1}, F ≥ f_{α/2,n1-1,n2-1}

Para un nivel de significación de: α = 0.05:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.05/2,15-1,20-1} = f_0.975,14,19 = 1/f_{1-0.975,19,14} = 1/f_0.025,19,14

· f_{α/2,n1-1,n2-1} = f_{0.05/2,15-1,20-1} = f_0.025,14,19

Buscamos en la tabla distribución F, con nivel de significación 0.05, pero el grado de libertad 14 y 19 en el primer miembro no se encuentra recogido en dichas tablas, por lo que interpolamos para obtener un valor aproximado:

· Para el grado de libertar 14:

..12.......14.......15
2.72.......P......2.62

De donde:

12 - 15.-> 2.72 - 2.62
12 - 14.-> 2.72 - P

Calculamos:

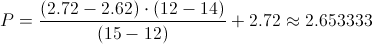
· Para el grado de libertar 19:

..15.......19.......20
2.95.......P......2.84

De donde:

15 - 20.-> 2.95 - 2.84
15 - 19.-> 2.95 - P

Calculamos:

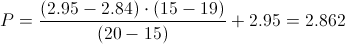
Por lo tanto, el valor de la región crítica es:

· f_0.975,14,19 = 1/f_0.025,19,14 = 1/2.862 ≈ 0.349406

· f_0.025,14,19 = 2.653333

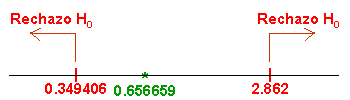
Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 0.656659 está dentro de la marcada por la región crítica, [0.349406, 2.862], por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que las varianzas de ambas compañías, son iguales.