Problema29: Estimación y Pruebas de Hipótesis

Ej29. Dos proveedores fabrican un engranaje de plástico utilizado en una impresora láser. Una característica importante de estos engranes, es la resistencia al impacto, la cual se mide en pies-libras.

Una muestra aleatoria de 10 engranes suministrados por el primer proveedor produce los siguientes resultados: X₁ = 290 y S²_c1 = 12.

Del segundo proveedor se toma una muestra aleatoria de 15 engranes, donde los resultados son: X₂ = 321 y S²_c2 = 15.

Determinar:

a) ¿Existe evidencia que apoye la afirmación de que los engranes del proveedor 2 tienen una media de resistencia al impacto mayor? Utilizar, α = 0.05 y suponer que las varianzas son iguales.

b) ¿Cuál es el p-valor de esta prueba?


Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Proveedor 1: n₁ = 10, X₁ =290, S²_c1 =12.
· Proveedor 2: n₂ = 15, X₂ =321, S²_c2 =15.
· Nivel de significación: α = 0.05.
· El tamaño de las muestras, n₁ y n₂, son menor o igual que 30, por lo tanto, hay que considerar poblaciones normales.

Pasamos a resolver los distintos apartados que nos plantea el problema.


Apartado a)

Teniendo en cuenta que el enunciado nos indica que ambas varianzas son iguales, calculamos lo que nos pide el problema: Contraste sobre diferencias de medias con varianzas desconocidas e iguales:

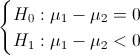
El estadístico es:

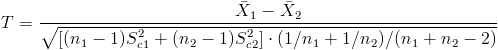
Obtenemos el valor del estadístico:

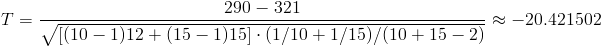
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

T ≤ - t_α,n1+n2-2

Para un nivel de significación de: α = 0.05:

· t_α,n1+n2-2 = t_0.05,10+15-2 = t_0.05,23

Buscamos en la tabla t-Student, con 23 grados de libertad y un nivel de significación 0.05, da como resultado, 1.7139.

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, -20.421502 es menor que el determinado por la región crítica, -1.7139, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto quiere decir que, existen evidencias significativas de que la media de la resistencia al impacto del proveedor 2 es mayor que la del proveedor 1.


Apartado b)

Nos piden obtener el p-valor, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existe una región crítica y la desigualdad de la hipótesis alternativa es: '< .', el p-valor en estas condiciones, se calcula cómo:

p-valor = P(T > |t|) = P(T > 20.421502)

Buscamos en las tablas de la t-Student con 23 grados de libertad, pero no encontramos el valor exacto para 20.421502, sólo el inferior más próximo, 3.7676, que corresponde a un área de cola de 0.0005.

Por lo tanto, el p-valor:

p-valor < .0.0005

Como el p-valor es menor que el nivel de significación, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto significa que, existen evidencias significativas de que la resitencia media al impacto del proveedor 2 es mayor que la del proveedor 1, ratificamos con esta prueba, la conclusión obtenida en el apartado anterior con la región crítica.