Problema28: Estimación y Pruebas de Hipótesis

Ej28. Doce hombres adultos, cuyas edades fluctúan entre 35 y 50 años, participan en un estudio para evaluar el efecto de la dieta y el ejercicio sobre los niveles de colesterol en la sangre.

El colesterol total fue medido al inicio en cada sujeto, y tres meses después de participar en un programa de ejercicio aeróbico y de haber cambiado a una dieta baja en grasas. Los datos son los siguientes:

Antes:	265..	240..	258..	295..	251..	245..	287..	314..	260..	279..	283..	240..
Después:	229	231	227	240	238	241	234	256	247	239	246	218

¿Apoyan estos datos la afirmación de que la dieta baja en grasas y el ejercicio aeróbico son de gran valor en la disminución del nivel de colesterol? Utilizar, α = 0.05.


En este problema, nos dan los datos de dos muestras aleatorias, por lo que tenemos que obtener la media de cada recopilación de datos.

Para obtener la media:

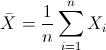
Por lo tanto:

· Antes:

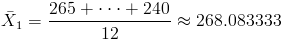
· Después:

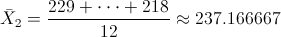
Para obtener la cuasi varianza:

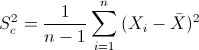
Por lo tanto, la cuasi varianza:

· Antes: S²_c1 ≈ 555.537879
· Después: S²_c2 ≈ 103.787879

Teniendo en cuenta que al ser el tamaño de las muestras n₁ y n₂ igual 12, por lo tanto, menor que 30, debemos considerar poblaciones normales.

Hay que tener en cuenta que para realizar la prueba de hipótesis de las medias, debemos conocer si las varianzas de ambas muestras aleatorias son iguales o distintas, el enunciado no nos dice nada al respecto por lo que debemos realizar, previamente, la prueba de hipótesis sobre la igualdad de varianzas de ambas muestras aleatorias.

La prueba de hipótesis de igualdad de varianzas:

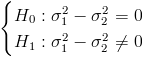
Es un contraste sobre igualdad de varianzas con medias desconocidas, el estadístico es:

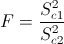
Obtenemos el valor del estadístico:

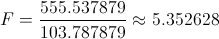
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

F ≤ f_{1-α/2,n1-1,n2-1}, F ≥ f_{α/2,n1-1,n2-1}

Para un nivel de significación de: α = 0.05, tenemos en la tabla distribución F:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.05/2,12-1,12-1} = f_0.975,11,11

· f_{α/2,n1-1,n2-1} = f_{0.05/2,12-1,12-1} = f_0.025,11,11

El grado de libertad 11, no está en las tablas de la distribución F que dispone Aqueronte, por lo que realizo la media:

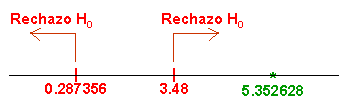
· f_{α/2,n1-1,n2-1} = f_0.025,11,11 = (3.53 + 3.43)/2 = 3.48

· f_{1-α/2,n1-1,n2-1} = f_0.975,11,11 = 1/f_{1-0.975,11,11} = 1/f_0.025,11,11 = 1/3.48 ≈ 0.287356

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 5.352628 está fuera del intervalo que compone la región crítica, (0.287356, 3.48), por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto quiere decir que, existen evidencias significativas de que las varianzas de ambas muestras, son diferentes.

Una vez conocidas que ambas varianzas son diferentes, calculamos lo que nos pide el problema: Contraste sobre diferencias de medias con varianzas desconocidas y distintas:

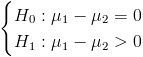
El estadístico es:

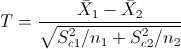
Obtenemos el valor del estadístico:

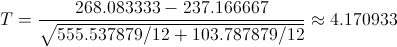
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

T ≥ t_α,v

Donde v:

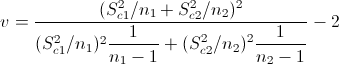
Sustituimos valores y obtenermos el valor de v:

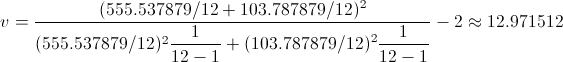
Por lo tanto, para un nivel de significación de: α = 0.05:

· t_α,v = t_{0.05, 12.971512}

En la tabla t-Student, no existe el grado de libertad 12.971512, por lo que realizamos una interpolación lineal para obtener un valor aproximado:

..12...........12.971512.......13
1.7823...........P.............1.7709

De donde:

12 - 13.-> 1.7823 - 1.7709
12 - 12.971512.-> 1.7823 - P

Calculamos:

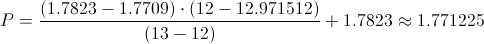
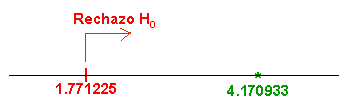
Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 4.170933 es mayor que el determinado por la región crítica, 1.771225, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto quiere decir que, existen evidencias significativas de que la dieta baja en grasas (la muestra aleatoria del después) y el ejercicio aeróbico son de gran utilidad en la disminución del nivel de colesterol.