Ej20. Un fabricante produce anillos para los pistones de un motor de automóvil. Se sabe que el diámetro del anillo está distribuido aproximadamente de manera normal, y que tiene una desviación estándar σ = 0,001 mm.
Una muestra aleatoria de 15 anillos tiene un diámetro promedio de X = 74.036 mm.
Determinar:
a) Un intervalo de confianza bilateral del 99% para el diámetro promedio del anillo.
b) Un límite inferior de confianza del 95% para el diámetro promedio del anillo.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· X ≡ 'Diámetro de anillos para los pistones de un motor de automóvil'.
· Sigue una distribución Normal: X ~ N(74.036, 0.001).
· Tamaño de la muestra: n = 15.
Pasamos a resolver los distintos enunciados del problema.
Apartado a)
En este problema nos pide realizar un intervalo de confianza para la media con varianza conocida y el tamaño de la muestra es menor que 30:
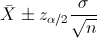
Para una confianza del 99%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.01. El siguiente paso es obtener el valor de la z:
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.495, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:
..2.57...........Z....... ..2.58
0.4949.....0.495.. .0.4951
De donde:
2.57 - 2.58.-> 0.4949 - 0.4951
2.57 - Z.-> 0.4949 - 0.495
Calculamos:
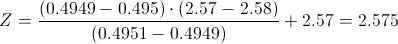
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 99%, simplemente, sustituimos valores:
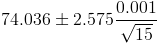
Apartado b)
En este problema nos pide realizar un intervalo de confianza unilateral inferior para la media con varianza conocida y el tamaño de la muestra es menor que 30:
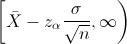
Para una confianza del 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.450, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:
..1.64...........Z....... ..1.65
0.4495.....0.450.. .0.4505
De donde:
1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z.-> 0.4495 - 0.450
Calculamos:
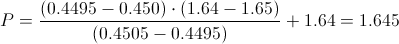
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo unilateral inferior de confianza de la media con un 95%, simplemente, sustituimos valores:
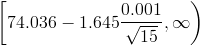





0 comentarios:
Publicar un comentario