Problema21: Estimación y Pruebas de Hipótesis

Ej21. Se utilizan dos máquinas para llenar botellas de plástico con detergente para máquinas lavaplatos. Se sabe, que las desviaciones estándar del volumen de llenado son σ₁ = 0,10 onzas de líquido y σ₂ = 0,15 onzas de líquido para las dos máquinas, respectivamente.

Se toman dos muestras aleatorias, n₁ = 12 botellas de la máquina 1 y n₂ = 10 botellas de la máquina 2.

Los volúmenes promedio de llenado son x₁ = 30,87 onzas de líquido y x₂ = 30,68 onzas de líquido.

a) Construya un IC bilateral del 90% para la diferencia entre las medias del volumen de llenado.

b) Construya un IC bilateral del 95% para la diferencia entre las medias del volumen de llenado. Compare el ancho de este intervalo con el ancho del cálculo en el inciso a).

c) Construya un IC superior del 95% para la diferencia de medias del volumen del llenado.



Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· X₁ ≡ 'Máquina 1'. Sigue una distribución Normal: X₁ ~ N(30.87, 0.10), n₁ = 12.
· X₂ ≡ 'Máquina 2'. Sigue una distribución Normal: X₂ ~ N(30.68, 0.15), n₂ = 10.

Pasamos a resolver los distintos apartados del problema.


Apartado a)

En este problema nos pide realizar un intervalo de confianza para la diferencia entre las medias con varianzas conocidas:

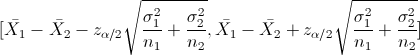
Para un 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.1/2 = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.45, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..1.64...........Z..... ..1.65
0.4495.....0.45.. .0.4505

De donde:

1.64 - 1.65 -> 0.4495 - 0.4505
1.64 - Z -> 0.4495 - 0.45

Calculamos:

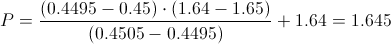
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 90%, simplemente, sustituimos valores:

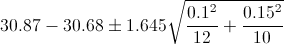
El intervalo de confianza bilateral al 90% es:

[0.098657, 0.281343]

Apartado b)

Este apartado es igual que el anterior pero, para un 95%. Obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.45, y dicho valor es z = 1.96.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:

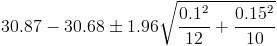
El intervalo de confianza bilateral al 95% es:

[0.081166, 0.298834]

Como podemos observar, si la probabilidad se aumenta, crece la amplitud del intervalo.


Apartado c)

Nos pide obtener un intervalo unilateral superior para el 95%, recopilamos los datos del apartado anterior para dicho nivel de significancia:

· α = 0.05.

Obtenemos el valor de z:

· z_α = z_0.05

Dicho valor ya lo hemos obtenido en el Apartado a) y es el siguiente:

· Z = 1.645

El intervalo de confianza unilateral superior es:

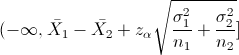
Como se puede apreciar, es la parte superior del intervalo del Apartado a) el que debemos calcular, por lo tanto, la solución es:

(-∞, 0.281343]