Ej22. Se prueban dos fórmulas diferentes de un combustible oxigenado para motor en cuanto al octanaje. La varianza del octanaje para la fórmula 1 es σ12 = 1.5, mientras que para la fórmula 2 es σ22 = 1.2.
Se prueban dos muestras aleatorias de tamaño n1 = 15 y n2 = 20. Los octanajes promedios observados son x1 = 89.6 y x2 = 92.5.
a) Construya un intervalo de confianza bilateral del 95% para la diferencia en el octanaje promedio.
b) ¿Qué tamaño de muestra se requiere para cada población si se desea tener una confianza del 95% de que el error al estimar la diferencia entre las medias de octanaje sea menor que 1?.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· X1 ≡ 'Fórmula 1'. Sigue una distribución Normal: X1 ~ N(89.6, √1.5), n1 = 15.
· X2 ≡ 'Fórmula 2'. Sigue una distribución Normal: X2 ~ N(92.5, √1.2), n2 = 20.
Pasamos a resolver los distintos apartados del problema.
Apartado a)
En este problema nos pide realizar un intervalo de confianza para la diferencia entre las medias con varianzas conocidas:
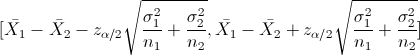
Para un 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:
· zα/2 = z0.05/2 = z0.025
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: Z = 1.96.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:
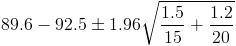
El intervalo de confianza bilateral al 95% es:
Apartado b)
En este apartado, nos piden obtener el tamaño de la muestra dado un error. Recopilamos datos del enunciado:
· Error: E < .1.
· Para un nivel del 95%.
Suponiendo n1 = n2 = n:
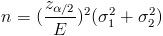
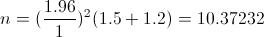
El tamaño de la muestra debe ser un número entero positivo, por lo tanto, la muestra tendrá tamaño 11.





1 comentarios:
Publicar un comentario