Problema23: Estimación y Pruebas de Hipótesis

Ej23. Un ingeniero civil hace pruebas con la resistencia a la comprensión del concreto. Para ello examina 12 especímenes y obtiene los siguientes datos:

2.216..	2.237..	2.249..	2.204
2.225	2.301	2.281	2.263
2.318	2.255	2.275	2.295

Construya un I.C. bilateral del 95% para la resistencia promedio.


En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.

Para obtener la media:

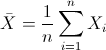
Por lo tanto:

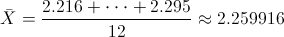
Para obtener la cuasi varianza:

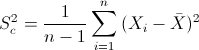
Por lo tanto, la cuasi desviación estándar:

S_c ≈ 0.035569

En este problema nos pide realizar un intervalo de confianza para la media con la varianza desconocida y el tamaño de la muestra menor que 30:

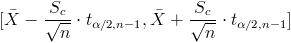
Para una confianza del 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05. Por lo tanto:

· t_α/2,n-1 = t_0.05/2,12-1=t_0.025,11

Buscamos el valor en la tabla t-Student, y obtenemos: 2.2010.

Ya disponemos todos los datos necesarios para obtener el intervalo bilateral de confianza al 95% del promedio con varianza desconocida y tamaño de la muestra menor que 30:

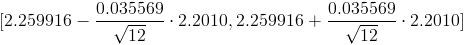
Por lo tanto:

[2.237316, 2.282516]