Problema24: Estimación y Pruebas de Hipótesis

Ej24. Se analiza la fracción de productos defectuosos producidos por dos líneas de producción. Una muestra aleatoria de 100 unidades provenientes de la línea 1 contiene 10 que son defectuosos, mientras que una muestra aleatoria de 120 unidades de la línea 2 tiene 25 que son defectuosas.

Encuentre un intervalo de confianza del 99% para la diferencia en fracciones de productos defectuosos producidos por las dos líneas.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· X₁ ≡ 'Línea 1'. Sigue una distribución Binomial: X₁ ~ B(100, 10/100) = B(100, 1/10).
· X₂ ≡ 'Línea 2'. Sigue una distribución Binomial: X₂ ~ B(120, 25/120) = B(120, 5/24).

Nos pide realizar un intervalo de confianza para la diferencia de fracciones con n₁ y n₂, mayor o igual que 30:

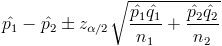
Para un 99%, obtenemos α:

100(1 - α) = 99

Despejamos el parámetro que nos interesa: α = 0.01. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.01/2 = z_0.005

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.005 = 0.495

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.495, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..2.57...........Z....... ..2.58
0.4949.....0.495.. .0.4951

De donde:

2.57 - 2.58.-> 0.4949 - 0.4951
2.57 - Z.-> 0.4949 - 0.495

Calculamos:

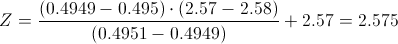
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la diferencia de fracciones de productos defectuosos producidos por dos líneas con un 99%, simplemente, sustituimos valores:

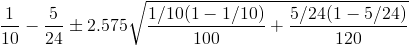
Por lo tanto:

[-0.231137, 0.014471]

Al contener el cero el intervalo de confianza hallado, no podemos obtener conclusiones significativas para la diferencia de fracciones de productos defectuosos producidos por dos líneas con un 99%.