Problema25: Estimación y Pruebas de Hipótesis

Ej25. Se utilizan dos máquinas para llenar botellas de plástico con un volumen neto de 16.0 onzas. Las distribuciones de los volúmenes de llenado pueden suponerse normales, con desviaciones estándar σ₁ = 0.020 y σ₂ = 0.025 onzas.

Un miembro del grupo de ingeniería de calidad sospecha que el volumen neto de llenado de ambas máquinas es el mismo, sin importar si éste es o no de 16 onzas. De cada máquina se toma una muestra aleatoria de 10 botellas.

Máquina 1:	16.03..	16.04..	16.05..	16.05..	16.02..	16.01..	15.96..	15.98..	16.02..	15.99
Máquina 2:	16.02	15.97	15.96	16.01	15.99	16.03	16.04	16.02	16.01	16.00

Determinar:

a) ¿Se encuentra el ingeniero en lo correcto? Utilice α = 0,05.

b) ¿Cuál es el valor P de esta prueba?.


En este problema, nos dan los datos de dos muestras aleatorias, por lo que tenemos que obtener la media de cada máquina.

Para obtener la media:

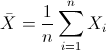
Por lo tanto:

· Máquina 1:

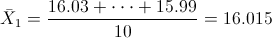
· Máquina 2:

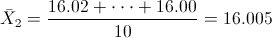
Realizamos una recopilación de los datos del problema:

· Tamaño de ambas muestras: n = 10.
· X₁ ≡ 'Máquina 1'. Sigue una distribución Normal: X₁ ~ N(16.015, 0.020).
· X₂ ≡ 'Máquina 2'. Sigue una distribución Normal: X₂ ~ N(16.005, 0.025).

Pasamos a resolver los distintos apartados del problema.


Apartado a)

La prueba de hipótesis que plantea el enunciado del problema es:

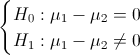
Es un contraste de diferencia de medias con desviación estándar conocida, el estadístico es:

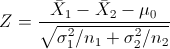
Obtenemos el valor del estadístico:

Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ - z_α/2, Z ≥ z_α/2

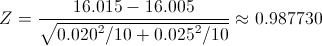
Para un nivel de significación de: α = 0.05, tenemos, en la tabla Normal:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: Z = 1.96.

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 0.987730 está dentro del intervalo que compone la región crítica, (-1.96, 1.96), por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que la diferencia de medias son iguales, por lo tanto, el ingeniero se encuentra en lo cierto.


Apartado b)

En este apartado, nos piden obtener el p-valor de la prueba del apartado anterior, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2 · P(Z > |z|) = 2 · P(Z > 0.987730) = 2·[1 - P(Z ≤ 0.987730)] = 2·[1 - (0.5 + Φ(0.987730))] = 2·[0.5 - Φ(0.987730)]

Buscamos en las tablas de la Normal, pero no encontramos el valor exacto para 0.987730, por lo que interpolamos linealmente:

..0.98...........0.987730.......0.99
0.3365...............P............0.3389

De donde:

0.98 - 0.99.-> 0.3365 - 0.3389
0.98 - 0.987730.-> 0.3365 - P

Calculamos:

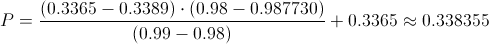
Sustituimos y obtenemos el p-valor:

p-valor = 2·[0.5 - Φ(0.987730)] = 2·[0.5 - 0.338355] = 0.32329

Como el p-valor es mayor que el nivel de significación, aceptamos la hipótesis nula.