Problema30: VAC

Ej30. La dureza Rockwell de un metal se determina al golpear con un punto acerado (herramienta) la superficie del metal y después medir la profundidad de penetración del punto.

Suponga que la dureza Rockwell de cierta aleación está normalmente distribuida con media de 70 y desviación estándar de 3 (la dureza Rockwell se mide en una escala continua).

Determinar:

a) Si un espécimen es aceptable sólo si su dureza está entre 67 y 75, ¿cuál es la probabilidad de que un espécimen seleccionado al azar tenga una dureza aceptable?.

b) Se la escala aceptable de dureza es (70 − c, 70 + c), ¿para qué valor de c tendría una dureza aceptable 95% de todos los especímenes?.


Realizamos una recopilación de los datos importantes que nos ofrece el enunciado del problema:

· X ≡ 'Dureza de Rockwell'.
· Sigue una distribución Normal: X ~ N(70, 3).

Pasamos a resolver los distintos apartados del problema.


Apartado a)

Nos piden obtener la probabilidad: P(67 ≤ X ≤ 75), tipifico a la normal:

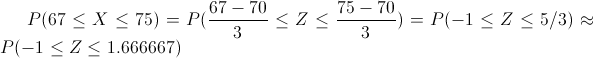
Por lo tanto:

P(-1 ≤ Z ≤ 1.666667) = [0.5 + Φ(1.666667)] - [1-(0.5 + Φ(1))]= Φ(1.666667) + Φ(1)

En este caso, no se dispone del valor exacto en las tablas, por lo tanto, interpolamos linealmente:

..1.66.............1.666667..........1.67
0.4515................P...............0.4525

De donde:

1.66 - 1.67.-> 0.4515 - 0.4525
1.66 - 1.666667..-> 0.4515 - P

Calculamos:

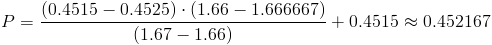
Por lo tanto, la solución a este apartado es:

P(-1 ≤ Z ≤ 1.666667) = Φ(1.666667) + Φ(1) = 0.452167 + 0.3413 = 0.793467

Apartado b)

En este apartado, debemos obtener el valor del parámetro c para que se cumpla la siguiente igualdad: P(70 - c ≤ X ≤ 70 + c) = 0.95, tipifico a la normal:

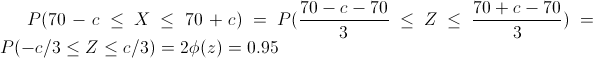
Despejamos Φ(z):

Φ(z) = 0.95/2 = 0.475

Buscamos en la tabla el valor 0.475 que de un z válido, en nuestro caso, obtenemos un valor exácto, el Z = 1.96.

Por lo tanto, el valor del parámetro c es:

1.96 = c/3

Despejamos c y obtenemos la solución a este problema: c = 5.88