Problema29: VAC

Ej29. Hay dos maquinas para cortar corchos destinados a usarse en botellas de vino. La primera produce corchos con diámetros normalmente distribuidos con media de 3 cm y desviación estándar de 0,1 cm.

La segunda máquina produce corchos con diámetros que tienen una distribución normal con media de 3,04 cm y desviación estándar de 0,02 cm.

Los corchos aceptables tienen diámetro entre 2,9 cm y 3,1 cm. ¿Cuál máquina tiene más probabilidad de producir un corcho aceptable?


Realizamos una recopilación de los datos importantes que nos ofrece el enunciado del problema:

· A₁ ≡ 'Máquina Primera'.
· A₂ ≡ 'Máquina Segunda'.
· Sigue una distribución Normal: A₁ ~ N(3, 0.1).
· Sigue una distribución Normal: A₂ ~ N(3.04, 0.02).
· El rango de diámetro aceptable del corcho es: [2.9, 3.1].
· Todos los datos en cm.


Nos piden que máquina tiene más probabilidad de fabricar corchos aceptables, por lo que debemos obtener la probabilidad de cada máquina en el intervalo de diámetros aceptables.

· Para la Máquina Primera:

Debemos hallar: P(2.9 ≤ A₁ ≤ 3.1), tipifico a la normal:

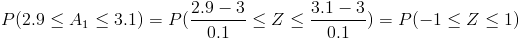
Por lo tanto:

P(-1 ≤ Z ≤ 1) = [0.5 + Φ(1)] - [1-(0.5 + Φ(1))]= 2·Φ(1)= 2·0.3413 = 0.6826

La probabilidad de que la Máquina Primera fabrique corchos dentro de las especificaciones dadas es de 0.6826.

· Para la Máquina Segunda:

Debemos hallar: P(2.9 ≤ A₂ ≤ 3.1), tipifico a la normal:

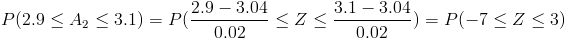
Por lo tanto:

P(-7 ≤ Z ≤ 3) = [0.5 + Φ(3)] - [1 - (0.5 + Φ(7))]= Φ(3) + Φ(7) ≈ 0.4987 + 0.5 = 0.9987

La probabilidad de que la Máquina Segunda fabrique corchos dentro de las especificaciones dadas es de 0.9987.


Por lo tanto, la mejor máquina es la segunda al ser su probabilidad de fabricar corchos dentro del interválo dado mayor.