Problema28: VAC

Ej28. Suponga que el error al hacer cierta medición es una variable aleatoria continua X con función de densidad:

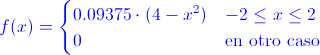
Hallar:

a) P(X > 0).

b) P(-1 ≤ X ≤ 1)


Lo primero que vamos a calcular, es la función de distribución acumulada:

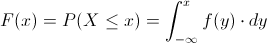
En nuestro caso, el intervalo que tenemos que realizar cálculos es -2 ≤ X ≤ 2:

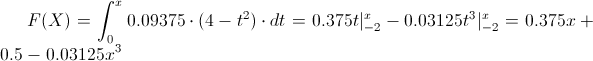
Por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:

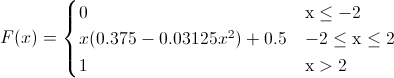
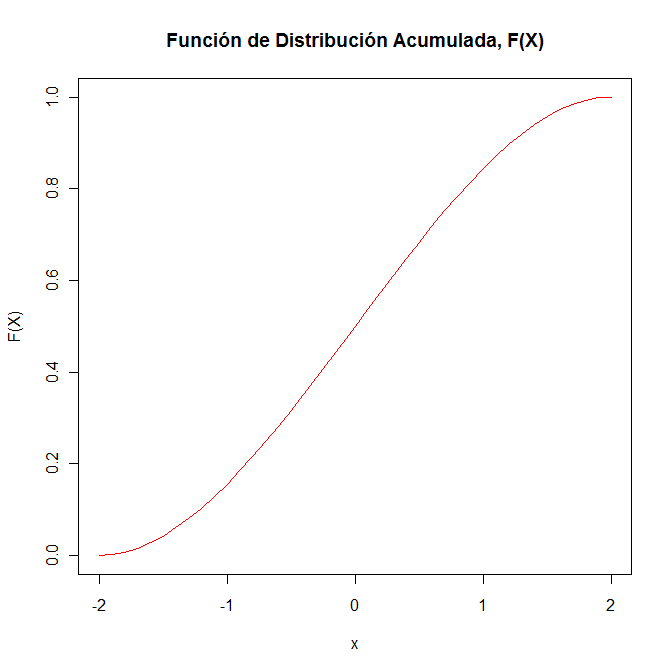
Para la representación gráfica de la función de distribución acumulada de la variable aleatoria continua X, se utilizará el programa R.

> x <- seq(-2,2,by=0.1)
> y = x*(0.375-0.03125*x^2)+0.5
> plot(x, y, type="l", xlab="x", ylab="F(X)", main="Función de Distribución Acumulada, F(X)", col=2)

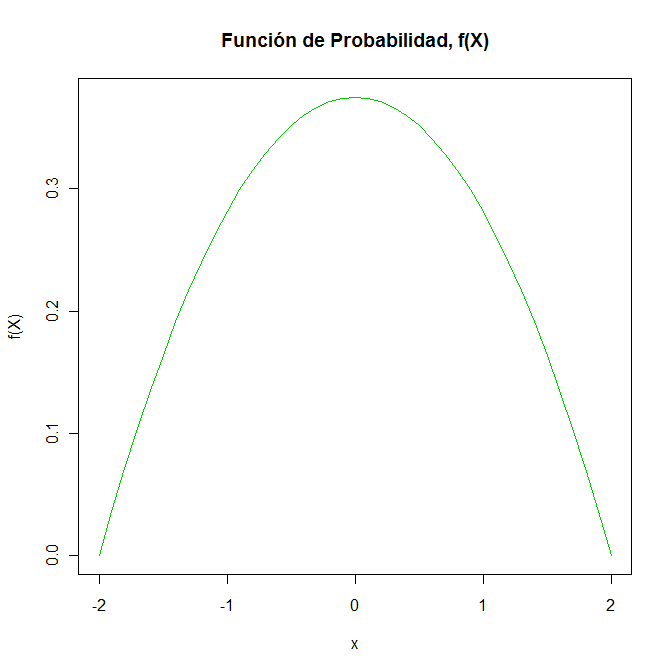
Para la representación gráfica de la función de densidad de probabilidad de la variable aleatoria continua X, se utilizará el programa R.

> x <- seq(-2,2,by=0.1)
> y = 0.09375*(4-x^2)
> plot(x, y, type="l", xlab="x", ylab="f(X)", main="Función de Densidad de Probabilidad, f(X)", col=3)

A partir de ahora, podemos pasar a resolver los distintos enunciados del problema.


Apartado a)

Para obtener la probabilidad dada, empleamos la expresión de la función de densidad acumulada en el intervalo: -2 ≤ X ≤ 2, por lo tanto:

P(X > 0) = 1 - P(X ≤ 0) = 1 - F(0) = 1 - 0.5 = 0.5

Apartado b)

Para obtener la probabilidad dada, empleamos, al igual que en el apartado anterior, la expresión de la función de densidad acumulada en el intervalo: -2 ≤ X ≤ 2, por lo tanto:

P(-1 ≤ X ≤ 1) = F(1) - F(-1) = (0.375 - 0.03125) + 0.5 + (0.375 - 0.03125) - 0.5 = 0.6875