Ej63. Un equipo de investigadores quiere estimar la proporción p de vacas que sufren el mal de las vacas locas en una explotación ganadera, mediante un intervalo con un error máximo de 0.015 y nivel de confianza al 95%.
¿A cuántas vacas deben analizar para alcanzar aproximadamente este objetivo, sabiendo que en un pequeño sondeo orientativo (muestra piloto) resultó que el 15% de las vacas estaban afectadas por la enfermedad?.
En este problema nos dan los datos de la proporción de vacas que estaban afectadas y el error máximo que podemos cometer para obtener el tamaño de la muestra necesaria que cumpla con estos requisitos.
El error para un intervalo de confianza de proporción es el siguiente:
El error para un intervalo de confianza de proporción es el siguiente:
Siendo:
· E = 0.015
· p = 0.15
· q = 1 - 0.15 = 0.85
Obtenemos el parámetro α: 100(1 - α) = 95, despejamos: α = 0.05
· z0.05/2 = z0.025
Teniendo en cuenta las condiciones de la tabla de la Normal que se exponen en este blog:
0.5 - 0.025 = 0.475
Buscamos en la tabla de la Normal y obtenemos el valor: z = 1.96.
Pues ya estamos en disposición de obtener el tamaño de muestra mínimo que cumpla con las especificaciones dadas, simplemente, despejamos el parámetro n y sustituimos valores:
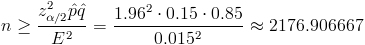
Por lo tanto, el tamaño mínimo muestral que se debe seleccionar para cumplir con los requisitos dados es de 2177 vacas.






1 comentarios:
Y que pasaría si te dicen que:
Un investigador desea estimar la proporción de “vacas locas” en una explotación con 100.000 vacas mediante un Intervalo de
Confianza del 95% y un error de estimación máximo de 0.015. ¿A cuántas vacas debe analizar sabiendo que, en una muestra piloto,
el 15% presentaban la enfermedad?
Publicar un comentario