Problema82: VAD

Ej82. Los pasajeros de las aerolíneas llegan al azar e independientemente a la sección de documentación en un gran aeropuerto internacional. La frecuencia promedio de llegadas es de 10 pasajeros por minuto.

Determinar:

a) ¿Cuál es la probabilidad de que no lleguen pasajeros en un minuto?

b) ¿Cuál es la probabilidad de que lleguen 3 pasajeros en un minuto?

c) ¿Cuál es la probabilidad de no llegadas en período de 15 segundos?

d) ¿Cuál es la probabilidad de al menos una llegada en período de 15 segundos?


Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de pasajeros que llegan a la sección de documentación de un gran aeropuerto internacional'.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(10) pasajeros/minuto.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.

Apartado a)

La probabilidad que debemos obtener es la siguiente:

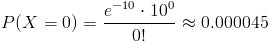
Por lo tanto, la probabilidad de que no llegue ningún pasajero es de, aproximadamente, 0.000045.

Apartado b)

La probabilidad que debemos obtener es la siguiente:

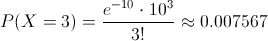
Por lo tanto, la probabilidad de que se lleguen tres pasajeros es de, aproximadamente, 0.007567.

Apartado c)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en un tiempo de 15 segundos:

..10.--- 60
..λ..--- 15

Por lo tanto, el número medio de pasajeros cada 15 segundos es:

· λ = (10·15)/60 = 2.5

La probabilidad que debemos obtener es la siguiente:

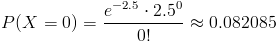
Por lo tanto, la probabilidad de que no se pase ningún pasajero cada 15 segundos es de, aproximadamente, 0.082085.

Apartado d)

Empleamos el parámetro promedio del apartado anterior. La probabilidad que debemos obtener es la siguiente:

P(X ≥ 1) = 1 - P(X < 1) = 1 - P(X = 0)

Sustituimos valores:

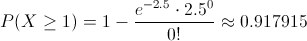
Por lo tanto, la probabilidad de que al menos, un pasajero se llegue cada 15 segundos es de, aproximadamente, 0.917915.