Ej64. Se efectúa un estudio sobre el color de los escarabajos tigre para conseguir pruebas que apoyen el argumento de que la proporción de escarabajos negros puede variar de un lugar a otro.
En una muestra de 500 escarabajos capturados en una extensión próxima a Providence, Rhode Island, 95 eran negros. Una captura de 112 escarabajos en Aqueduct, Nueva York, contenía 17 individuos negros.
A la vista de estos datos, ¿qué se puede decir sobre el argumento anterior?
NOTA: Suponer normalidad con α = 0.05.
Realizamos una recopilación de datos que nos ofrece el enunciado del problema.
● Providence, Rohde Island:
· ṗ1 = 95/500 = 0.19.
· n1 = 500.
● Aqueduct, New York:
· ṗ2 = 17/112.
· n2 = 112.
Debemos realizar un contraste sobre diferencia de proporciones, pero para ello, se deben cumplir las siguientes condiciones:
· n1·ṗ1 = 500·0.19 = 95 ≥ 5...OK
· n1·(1 - ṗ1) = 500·(1 - 0.19) = 405 ≥ 5...OK
· n2·ṗ2 = 112·17/112 = 17 ≥ 5...OK
· n2·(1 - ṗ2) = 112·(1 - 17/112) = 95 ≥ 5...OK
· n1 = 500 ≥ 30.. OK
· n2 = 112 ≥ 30...OK
Se cumplen todos los requisitos.
Prueba de hipótesis sobre diferencia de proporciones: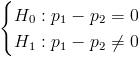
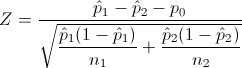
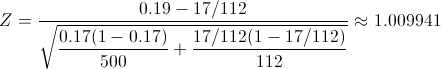
Teniendo en cuenta las condiciones de la tabla que dispone este blog, adecuamos el valor:
Buscamos en la tabla de la Normal y tenemos el valor: z = 1.96.
Realizamos una concepción gráfica de los datos hasta ahora obtenidos:
Esto quiere decir que, existen evidencias significativas de que la proporción de escarabajos negros es la misma en ambos sitios.
sábado, 25 de septiembre de 2010
Problema64: Estimación y Pruebas de Hipótesis
El estadístico es:
Obtenemos el valor del estadístico:
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
Z ≤ -zα/2 , Z ≥ zα/2
Para un nivel de significación de: α = 0.05, tenemos, en la tabla Normal:
· zα/2 = z0.05/2 = z0.025
0.5 - 0.025 = 0.475
El valor del estadístico, 1.009941 se encuentra dentro de la región crítica (-1.96, 1.96), por lo tanto, aceptamos la hipótesis nula
Publicado por el barquero
Unknown
en
23:08
![]()
Etiquetas: Estadística, Matemáticas, Problemas
Suscribirse a:
Enviar comentarios (Atom)






0 comentarios:
Publicar un comentario