Ej65. Los investigadores de la Environmental Protection Agency (EPA) se interesan por la calidad del aire. Uno de los indicadores de la calidad del aire es el número medio de microorganismos de partículas en suspensión por metro cúbico de aire.
Es decir, el interés se centra en la media de la variable aleatoria X, número de microorganismos de partículas en suspensión por metro cúbico de aire. Para controlar la situación se hace una lectura cada seis días, extrayendo un metro cúbico de aire a través de un filtro y determinado el número de microorganismos de partículas en suspensión concentradas en él.
Después de un período de treinta días, se ha generado una muestra aleatoria de tamaño 5.
Supóngase que los valores observados de estas variables, para el período dado de 30 días son:
| 58. | 57. | 59. | 70. | 61. |
a) Es conocido por experiencias previas que la variable en estudio está normalmente distribuida con desviación típica poblacional igual a 9.
b) Es conocido por experiencias previas que la variable en estudio está normalmente distribuida.
En este problema, nos dan los datos de una muestra aleatoria, obtendremos la información que nos será necesaria para la resolución de este problema.
El tamaño de la muestra es:
· n = 5
Para obtener la media:
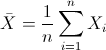
Por lo tanto:
·
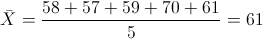
Para obtener la cuasi varianza:
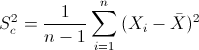
Por lo tanto, la cuasi desviación típica:
· Sc ≈ 5.244044
Para una confianza del 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05.
Pasamos a resolver los distintos apartados que nos ofrece el problema.
Apartado a)
En este problema nos pide realizar un intervalo de confianza para la media con varianza conocida y el tamaño de la muestra es menor que 30:
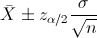
El siguiente paso es obtener el valor de la z:
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: z = 1.96.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:
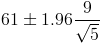
El intervalo de confianza bilateral al 95% es:
Apartado b)
En este problema nos pide realizar un intervalo de confianza para la media con varianza desconocida y el tamaño de la muestra es menor que 30:
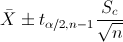
El siguiente paso es obtener el valor de la t-Student:
· tα/2,n-1 = t0.05/2, 5-1 = t0.025, 4
Buscamos el valor en la tabla t-Student, y obtenemos: 2.7765.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:
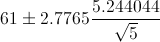
El intervalo de confianza bilateral al 95% es, aproximadamente:





3 comentarios:
Hola.
Quisiera primeramente felicitarle por este magnífico blog, el cual es una maravilla para todos aquellos amantes de la Estadística y para los estudiantes de la misma.
Simplemente, una pequeña duda que tengo sobre el enunciado:
- En el apartado a), nos dan como dato la varianza poblacional (en este caso igual a 9), es decir, "sigma" elevada al cuadrado, y no "sigma" que es como está en la resolución del ejercicio,¿me equivoco? Por lo tanto el resultado no sería del todo correcto.
Un saludo
Buenas:
Tienes toda la razón del mundo, el problema es que no se si el enunciado de este problema fue diseñado por mí o no, entonces ahora, no se si está mal el enunciado o la resolución del apartado.
Para no tener que cambiar y rehacer la expresión matemática de dicho apartado, voy a cambiar el enunciado y en vez de poner varianza poblacional, que sea desviación típica poblacional.
Me alegro que te sea de ayuda este blog y darte las gracias por avisarme del error.
Un saludo y muchísimas gracias.
¿Si no me dicen que se comporta como una distribución normal, y no lo puedo suponer, como se resuelve? (pero si me dan la varianza = 9)
Publicar un comentario