Problema81: VAD

Ej81. Un embarque de 10 artículos contiene 2 unidades defectuosas y 8 no defectuosas. Al revisarlo, se tomará una muestra y las unidades se inspeccionarán.

Si se encuentra una unidad defectuosa, se rechazará todo el embarque.

a) Si se selecciona una muestra de 3 artículos. ¿Cuál es la probabilidad de rechazar el embarque?.

b) Si se selecciona una muestra de 4 artículos. ¿Cuál es la probabilidad de rechazar el embarque?.


Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de artículos defectuosos'.
· La variable aleatoria X sigue una distribución Hipergeométrica: X ~ HG de parámetros:
· Número total de unidades: N = 10.
· Tamaño de la muestra: n = 2. (Número total de unidades con defectos)
· Se rechaza el embarque completo si al menos hay un artículo defectuoso.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)


Debemos hallar la siguiente probabilidad:

P(X ≥ 1) = 1 - P(X < 1) = 1 - P(X = 0)

Teniendo en cuenta:

· Número total de unidades seleccionadas aleatoriamente: r = 3.

Por lo tanto, la probabilidad de que se rechace el embarque completo teniendo en cuenta que se han seleccionado tres muestras es de, aproximadamente, 0.533333.


Apartado b)


Debemos hallar la siguiente probabilidad:

P(X ≥ 1) = 1 - P(X < 1) = 1 - P(X = 0)

Teniendo en cuenta:

· Número total de unidades seleccionadas aleatoriamente: r = 4.

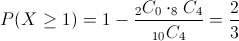
Por lo tanto, la probabilidad de que se rechace el embarque completo teniendo en cuenta que se han seleccionado cuatro muestras es de, aproximadamente, 0.666667.