Problema15: Estimación y Pruebas de Hipótesis

Ej15. Existen dos tipos de plásticos apropiados para su uso por un fabricante de componentes electrónicos. La tensión de ruptura de este plástico es un parámetro muy importante. Se sabe que las desviaciones estándar de dos muestras son iguales y de valor 1 psi.

La muestra aleatoria primera tiene un tamaño de 10 y la segunda muestra aleatoria tiene un tamaño de 12, la media de la primera es 162.5 psi y de la segunda es 155 psi.

La compañía no adoptará el plástico primero a menos que la tensión de ruptura de éste, exceda a la del plástico segundo, al menos por 10 psi.

En base a la información contenida en la muestra, ¿deberá la compañía utilizar el plástico primero? El nivel de significación es de 0.05.


Realizamos una recopilación de los datos del problema:

· Plástico 1: n1 = 10, X1 = 162.5, σ1 = 1.
· Plástico 2: n2 = 12, X2 = 155, σ2 = 1.

Para determinar si la compañía debe adoptar el plástico 1, emplearemos una prueba de hipótesis de las diferencias de medias con varianzas conocidas:

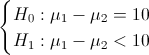
Cuyo estadístico es:

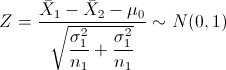
Sustituimos valores y obtenemos el valor del estadístico:

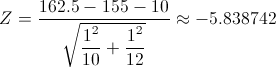
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ - z_α

Para un nivel de significación de: α = 0.05, tenemos:

· z_α = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.450

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.450, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..1.64...........Z..... ..1.65
0.4495.....0.450.. .0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z.-> 0.4495 - 0.450

Calculamos:

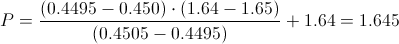
Comprobamos el valor del estadístico con la región crítica:

-5.838742 ≤ - 1.645

Se cumple la condición de la región crítica, por lo tanto, rechazamos la hipótesis nula y aceptamos la alternativa.

Esto indica que la diferencia de medias del plástico 1 y del plástico 2 no difieren al menos en 10 psi, sino en menos, por lo tanto, la compañía no deberá utilizar el plástico 1.