Ej14. La pintura para autopista se surte en dos colores: blanco y amarillo. El interés se centra en el tiempo de secado de la pintura. Se sospecha que la pintura de color amarillo se seca más rápidamente que la blanca.
Se obtienen mediciones de ambos tipos de pintura, que dan los siguientes tiempos de secado, en minutos:Blanca 120. 132. 123. 122. 140. 110. 120. 107 Amarilla 126 124 116 125 109 130 125 117 129 120
Encuentre un intervalo de confianza del 95% para la diferencia entre los tiempos de secados medios, suponiendo que las desviaciones estándar de éstos son iguales. ¿Existe alguna evidencia que indique que la pintura amarilla seca más rápidamente que la blanca?
Nos piden obtener un intervalo de confianza para la diferencia de medias con varianzas desconocidas e iguales, por lo tanto, debemos usar:
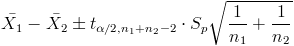
Obtenemos los valores de los parámetros necesarios.
Para obtener la media:
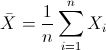
Para cada muestra de pintura:
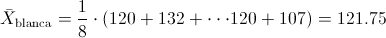
·
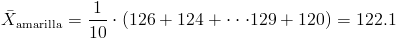
Para obtener la cuasi varianza:
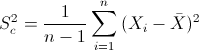
Para cada muestra de pintura:
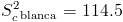
·
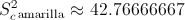
Necesitamos obtener el valor de Sp:
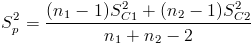
Sustituimos valores y obtenemos su valor:
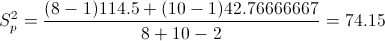
Para una confianza del 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05. Por lo tanto:
Buscamos el valor en la tabla t-Student, y obtenemos: 2.1199.
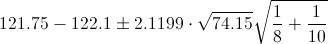
El intervalo de confianza bilateral al 95% es:





5 comentarios:
¿Faltaría parte del enunciado?
Muchas gracias por el blog.
Buenas:
El enunciado está completo para la realización del ejercicio, ¿a qué te refieres con que faltaría parte del enunciado del problema?
Un saludo.
las desviaciones estan incorrectas lo demas perfecto !
Buenas:
Acabo de comprobar las cuasi-varianzas y están correctas.
Un saludo.
las desviaciones estándar están erróneas, comprobar con la calculadora ya que tomó el valor sx y no rx
Publicar un comentario