Problema16: Estimación y Pruebas de Hipótesis

Ej16. Se sabe que el diámetro de los agujeros para una montura de cable tiene una desviación estándar de 0.01 pulgadas. Se obtiene una muestra aleatoria de 10 monturas, donde el diámetro promedio resulta ser 1.5045 pulgadas. Utilizando un nivel de significación de 0.01, determinar:

a) Prueba de hipótesis de que el diámetro medio verdadero del agujero es de 1.5 pulgadas.

b) ¿Cuál es el p-valor de esta prueba?


Realizamos una recopilación de los datos del problema:

· Tamaño de la muestra: n = 10.
· Diámetro promedio: X = 1.5045.
· Desviación estándar: σ = 0.01.
· Nivel de significación: α = 0.01.


Apartado a)

Nos piden realizar una prueba de hipótesis de que el diámetro medio verdadero, es de 1.5 pulgadas, con varianza conocida:

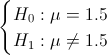
Cuyo estadístico es:

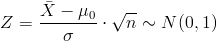
Sustituimos valores y obtenemos el valor del estadístico:

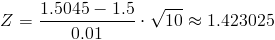
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ - z_α/2 , Z ≥ z_α/2

Para un nivel de significación de: α = 0.01, tenemos:

· z_α/2 = z_0.01/2 = z_0.005

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.005 = 0.495

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.495, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..2.57...........Z..... ..2.58
0.4949.....0.495.. .0.4951

De donde:

2.57 - 2.58.-> 0.4949 - 0.4951
2.57 - Z.-> 0.4949 - 0.495

Calculamos:

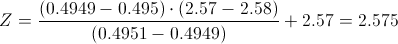
Comprobamos el valor del estadístico con la región crítica:

No se cumplen las condiciones de la región crítica, por lo tanto, aceptamos la hipótesis nula.

Esto indica que existen evidencias de que el diámetro medio verdadero del agujero es de 1.5 pulgadas.


Apartado b)

En este apartado, nos piden obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2·P(Z > |z|) = 2·P(Z > 1.423025) ≈ 2·P(Z > 1.423)

Operamos la desigualdad:

p-valor = 2·[1 - P(Z ≤ 1.423)] = 2·[1 - (0.5 + Φ(1.423))] = 2·[0.5 - Φ(1.423)]

Buscamos en las tablas de la Normal, pero no encontramos el valor exacto para 1.423, por lo que interpolamos linealmente:

..1.42...........1.423.......1.43
0.4222............P.........0.4236

De donde:

1.42 - 1.43.-> 0.4222 - 0.4236
1.42 - 1.423.-> 0.4222 - P

Calculamos:

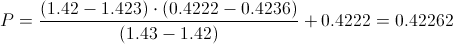
Sustituimos y obtenemos el p-valor:

p-valor = 2·[1 - (0.5 + Φ(1.423))] = 2·[0.5 - 0.42262] = 0.15476

Como el p-valor es mayor que el nivel de significación, aceptamos la hipótesis nula. Hay que tener en cuenta, que el parámetro del p-valor es una prueba más fuerte que los intervalos de confianza.