Problema36: Estimación y Pruebas de Hipótesis

Ej36. Una empresa dedicada al montaje de equipos informáticos distribuye entre sus clientes dos modelos: A y B. Cierto estudio de mercado concluyó que al menos tres de cada cuatro individuos del grupo de clientes potenciales preferían el modelo A.

Un estudio paralelo del departamento de análisis de datos de la empresa mostró que, de 1000 individuos tomados al azar entre los clientes del último año, 700 compraron el modelo A.

Si el comportamiento de los antiguos clientes se puede extrapolar al del grupo de clientes potenciales, ¿avala este último estudio las conclusiones del estudio de mercado realizado?

Tómese un nivel de signifi cación α = 0.01.


Realizamos una recopilación de datos del problema:

· Tamaño de la muestra: n = 1000.
· Individuos que compraron el modelo A: 700.
· Proporción de de individuos que compraron el modelo A: ṗ = 700/1000 = 0.7.
· Nivel de significación: α = 0.01.
· A ≡ 'Prefiere el modelo A'.
· p(A) = p_o = 3/4 = 0.75.

La prueba de hipótesis que plantea el enunciado del problema es:

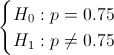
Es un contraste sobre la proporción, el estadístico es:

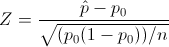
Obtenemos el valor del estadístico:

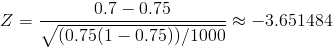
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≥ Z_α/2, Z ≤ -Z_α/2

Para un nivel de significación de: α = 0.01, tenemos, en la tabla Normal:

· Z_α/2 = Z_0.01/2 = Z_0.005

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.005 = 0.495

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.495, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..2.57...........Z....... ..2.58
0.4949.....0.495.. .0.4951

De donde:

2.57 - 2.58.-> 0.4949 - 0.4951
2.57 - Z.-> 0.4949 - 0.495

Calculamos:

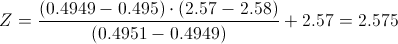
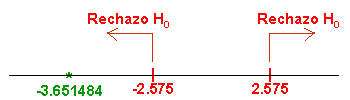
Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, -3.651484 está fuera de la región crítica, [-2.575, 2.575], por lo tanto, rechazamos la hipótesis nula.

Esto quiere decir, que existen evidencias significativas de no avalar el último estudio de mercado realizado.


Ahora, obtendremos el p-valor, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2 · P(Z > |z|) = 2 · P(Z > 3.651484) = 2 · [1 - P(Z ≤ 3.651484)] ≈ 2 · [1 - (0.5 + Φ(3.65))] = 2 · [0.5 - Φ(3.65)]

Buscamos en las tablas de la Normal, el valor para 3.65, es: z = 0.4999.

Sustituimos y obtenemos el p-valor:

p-valor = 2 · [0.5 - Φ(3.65)] = 2·[0.5 - 0.4999] = 0.0002

Como el p-valor es menor que el nivel de significación, rechazamos la hipótesis nula, y por ende, se acepta la hipótesis alternativa.