Problema35: Estimación y Pruebas de Hipótesis

Ej35. De una variable con distribución normal se obtuvo la siguiente muestra aleatoria:

-3.

-2.5.

-2.

-1.

1.

2.

2.5.

3..

Contraste la hipótesis nula de que la varianza es 5 frente a la alternativa de que es mayor. Tome un nivel de signifi cación de α = 0.05.


En este problema, nos dan los datos de una muestra aleatoria, obtendremos la información que nos será necesaria para la resolución de este problema.

El tamaño de la muestra es:

· n = 8

Para obtener la media:

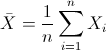
Por lo tanto:

·

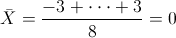
Para obtener la cuasi varianza:

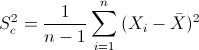
Por lo tanto, la cuasi varianza es:

· S²_c ≈ 5.785714

La prueba de hipótesis que plantea el enunciado del problema es:

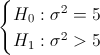
Es un contraste de varianza con media desconocida y sigue una distribución normal, el estadístico es:

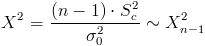
Obtenemos el valor del estadístico:

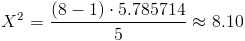
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

X² ≥ X²_{α, n-1}

Para un nivel de significación de: α = 0.05, tenemos, en la tabla ji-Cuadrada:

· X²_{α, n-1} = X²_{0.05, 8-1} = X²_{0.05, 7} = 14.07

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 8.10 es menor que el valor de la región crítica, 14.07, por lo tanto, aceptamos la hipótesis nula. Esto quiere decir, que existen evidencias significativas de que la varianza de la muestra planteada por el enunciado del problema es de valor 5.

Ahora, vamos a obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, la hipótesis alternativa evalúa si es mayor el valor del estadístico, por lo tanto, tenemos una cola de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = P(X² > x²)

Buscamos en las tablas de la ji-Cuadrada con 7 grados de libertad, no encontramos el valor exacto, pero está dentro de los valores: 6.35 < . 8.10 < . 8.38, cuya área de cola corresponde a: 0.3 < . α < . 0.5.

Por lo tanto, el p-valor estará comprendido entre los valores:

0.3 < . p-valor < . 0.5

Podemos dar un valor aproximado del p-valor realizando una interpolación lineal:

.0.300......X.......0.500
..8.38.....8.10......6.35

De donde:

0.300 - 0.500.-> 8.38 - 6.35
0.300 - X.-> 8.38 - 8.10

Calculamos:

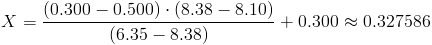
Por lo tanto, el p-valor es:

p-valor = P(X² > 8.10) = 0.327586

Conclusión, el nivel de significación, α = 0.05, es más pequeño que el p-valor, por lo tanto, aceptamos la hipótesis nula.

Aceptar la hipótesis nula quiere decir que en la varianza de la muestra del problema, existen evidencias significativas de que su varianza sea de valor 5.