Problema34: Estimación y Pruebas de Hipótesis

Ej34. Del tiempo que funciona cierto componente de un sistema hasta que comienza a presentar fallos sistemáticos se sabe que sigue una distribución normal. A fi n de estimar el tiempo medio de funcionamiento a pleno rendimiento, se observaron 10 de estas componentes obteniéndose los siguientes tiempos, en miles de horas, de funcionamiento sin fallos:

1.

1.5.

0.8.

1.2.

0.9.

1.1.

1.4.

1.3..

0.7..

0.1

Obtener un intervalo de con fianza, al 90%, para el tiempo medio de funcionamiento.


En este problema, nos dan los datos de una muestra aleatoria, obtendremos la información que nos será necesaria para la resolución de este problema.

El tamaño de la muestra es:

· n = 10

Para obtener la media:

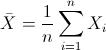
Por lo tanto:

·

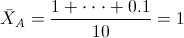
Para obtener la cuasi varianza:

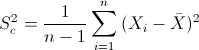
Por lo tanto, la cuasi desviación típica:

· S_c ≈ 0.408248

En este problema nos pide realizar un intervalo de confianza para la media con varianza desconocida y el tamaño de la muestra es menor que 30:

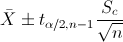
Para una confianza del 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la t:

· t_α/2,n-1 = t_0.1/2,10-1 = t_0.05,9

Buscamos el valor en la tabla t-Student, y obtenemos: 1.8331.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 90%, simplemente, sustituimos valores:

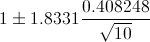
El intervalo de confianza bilateral al 90% es:

[0.763348, 1.236652]